|
+ | |
+ | |
+ | |
+ | |
+ | |
+ | |
+ ... = ? | Eq. (0) |
ABSTRACT: We construct an advanced model for interacting multiple stellar systems in which we compute all trajectories with a numerical N-body integrator, namely the Bulirsch-Stoer from the SWIFT package. We can then derive various observables: astrometric positions, radial velocities, minima timings (TTVs), eclipse durations, interferometric visibilities, closure phases, synthetic spectra, spectral-energy distribution, and even complete light curves. We use a modified version of the Wilson-Devinney code for the latter, in which the instantaneous true phase and inclination of the eclipsing binary are governed by the N-body integration.
If one has all kinds of observations at disposal, a joint A χ2 ($\chi^2$) metric and an optimisation algorithm (a simplex or simulated annealing) allows to search for a global minimum and construct very robust models of stellar systems. At the same time, our N-body model is free from artefacts which may arise if mutual gravitational interactions among all components are not self-consistently accounted for.
Finally, we present a number of examples showing dynamical effects that can be studied with our code and we discuss how systematic errors may affect the results (and how to prevent this from happening).
Recently, the model was adapted for solar-system applications,
e.g., observations of asteroid moons.
In particular, we implemented:
(i) a fitting of relative astrometry,
(ii) angular velocities,
(iii) adaptive-optics silhouettes,
(iv) variable distance,
(v) variable geometry (u, v, w),
(vi) brute-force algorithm,
(vii) multipole development (up to l = 10), and
(viii) external tide.
A detailed description and its application for (216) Kleopatra was published in
Brož et al. (2021), A&A 653, A56.
(See also Marchis et al. (2021), A&A 653, A57.)
data_20200922_SKY3.tar.gz xitau_20210322_360DEG.tar.gz 216_fitting33_360DEG__368.tar.gz gravity9_EQUIPOTENTIALS.tar.gzAn extension of this model including tidal evolution was published in Brož et al. (2022), A&A 657, A76.
xitau_20210401_MIGNARDQ.tar.gz 216_fitting36_MIGNARDQ__360.tar.gzAn application to (22) Kalliope was published in Ferrais et al. (2022), A&A 662, A71.
data_20211019_carry.tar.gz xitau_20210913_NOTDPC.tar.gz 22_test8_MULTIOCC_ROTZ__226.tar.gzA description of precise photometric algorithms - polygonal and `cliptracing' - was published in Brož et al. (2023), A&A 676, A60.
data_20221110_trappist.tar.gz data_20221122_damit.tar.gz data_20221128_occultation.tar.gz data_20221205_descamps.tar.gz data_20221208_korea.tar.gz xitau_20230117_HAPKE.tar.gz 22_test48_update__6695.tar.gz 22_fitting10_GRIDC20__249.tar.gz xitaushp_20230130_VARIEG.tar.gz 22_test51_ellipsoid__4195.tar.gz xitau_20240124_POLYS.tar.gz 22_test48_update__6718.tar.gzAn application to (130) Elektra was published in Fuksa et al. (2023), A&A 677, A189.
data_20230203_ephemeris.tar.gz 130_fitting4_6thorder__920.tar.gz
See the most recent vers. on [Github].
| Figure 1: The orientation of orbits, moon positions, velocities, and Kleopatra orientation. The output time step was 1/2 hour. Observational circumstances: Sun below horizon, astronomical night, Kleopatra above horizon, airmass < 1.6. It is quite restrictive; the minimum altitude 39° (cf. airmass) vs. the maximum 55°. The moons are required to be about: 90° shifted in true longitude (due to different multipole perturbations); separated from Kleopatra (no eclipses!); not stationary, or low-angular-speed; orbits should be as opened; of course, the angular size should be the largest (although it does not change much from Aug-Oct 2022). |
 |
| Figure 2: Occultation of TYC 13-01531-1 by (216) Kleopatra on Jan 21st 2023 19:51 UTC, which will be observable in Portugal--Spain--Italy. The moon shadows will be located Spain--France--Italy (outer), or Morocco--Algeria--Tunisia (inner), respectively. The (external) JPL ephemerides were used for the geocentric trajectory, and the (external) Gaia DR3 astrometric positions of the respective star. In Xitau, we computed the best-fit trajectories of the moons, and applied the proper motion, parallax, TDB→UT1 transformation, light time, precession, nutation, an intersection with the WGS-84 ellipsoid, as well as the Earth rotation (GST). All of them affect the topocentric shadow position substantially (>5 km). |
The original model description was published in Brož (2017), ApJS 230, 19. Moreover, an unoffcial Appendix C briefly describes dynamical effects that can be expected in N-body simulations. An application to the ξ Tauri system was described in Nemravová et al. (2016), A&A 594, A55. A new vers. also calls Pyterpol to generate synthetic spectra.
data_20160413_GAMMA.tar.gz data_20160331_CLOSUREPHASE.tar.gz data_20160415_AMBER.tar.gz data_20160524_SYNTHETIC.tar.gz data_20160612_UBV.tar.gz xitau_simplex_chi2_GAMMA_201604131719.tar.gz xitau_simplex_chi2_CLOSUREPHASE_201604131705.tar.gz xitau_simplex_chi2_PERIOD_201704081157.tar.gzAn application to the V746 Cas system was published in Harmanec et al. (2018), A&A 609, A5.
data_20170802_TELLURIC.tar.gz xitau_simplex_chi2_HEC88_201708041001.tar.gzAn application to the QZ Carinae system was published in Brož et al. (2022), A&A 666, A24.
data_20211213_vizier.tar.gz data_20220125_outliers.tar.gz data_20220128_litpro.tar.gz data_20220131_feros.tar.gz xitau_20220606_OCCULT.tar.gz qzcar_test38_nominal__630856.tar.gzAn application to the δ Orionis system was published in Oplištilová et al. (2023), A&A, 672, A31.
data_20220314_wdsall.tar.gz data_20220318_most.tar.gz data_20220325_spectra.tar.gz data_20220822_amdlib.tar.gz data_20220926_hvar.tar.gz xitau_20220929_C20.tar.gz deltaori_test41_C20__23739.tar.gz deltaori_test44_52.0MS__25468.tar.gz deltaori_fitting8_LOGGGRID.tar.gz
See the most recent vers. on [Github].
Additional programs, namely: Pyterpol for Python3, grids of synthetic spectra, and the Bulirsch-Stoer integrator with digital filters for long-term simulations.
pyterpol3_20220121.tar.gz grids.tar.gz grids_ABS.tar.gz POWR_Z_1.0.tar.gz TEST.tar.gz swift_bs_fp_201606032142.tar.gz old_versions/
 |
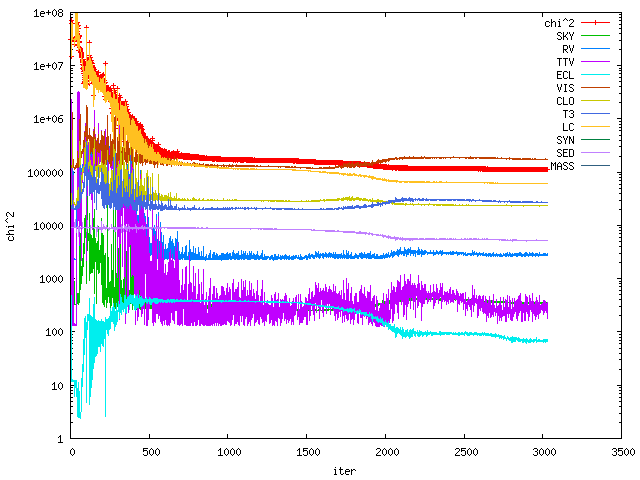| Figure 3: A χ2 ($\chi^2$) vs the number of iterations, showing a smooth convergence of simplex to a local minimum. We can distinguish individual contributions to χ2, namely astrometry (SKY), radial velocities (RV), minima timings (TTV), eclipse durations (ECL), squared visibilities (VIS), closure phases (CLO), triple product amplitude (T3), light curve (LC), synthetic spectra (SYN), spectral-energy distribution (SED), and additional mass constraints (MASS; actually not visible). |
 |
| Figure 4: Contributions to chi^2 for a set 64 best-fit models of QZ Car. Individual contributions (datasets) are shown in the panels (from top left): TTV, RV, SKY2, SED, SYN, VIS, CLO, T3. Every convergence was initialized with a different combination of masses m1, m2 (Ac1, Ac2), within in the range 15 to 50 M_S, while m3 (Aa1) was set to m_sum-m1-m2-m4; nevertheless, all parameters were free during convergence. Axes correspond to the masses m1, m2, colours to chi^2 (cf. tiny numbers), with adapted colour scales: cyan the very best fit for dataset, blue good fits (<1.2 min chi^2), orange poor fits (≥ 1.2 min chi^2). The factor was 3.0 for TTV, RV, SKY2. 'Forbidden regions' can be clearly seen (e.g., low m1, m2 especially due to CLO), as well as correlations between parameters (TTV -, RV +). The weighted very best fit for all datasets is denoted by the red circle. |