 |
 |
 |
swift_rmvsy.f program is based on swift.tar.Z package, which is available at ftp://gort.space.swri.edu.
I have modified subroutine getacch.f for the accelaration calculation and added Yarkovski diurnal effect. The new subroutines were developed: io_init_th.f (read in thermal data), and low-pass filter applied on output orbital elements: io_init_filter.f (read in filter parameters), io_write_filter.f (accumulate orbital elements in a buffer, if buffer is filled up, filter the data and write binary output file). For more details on filtering/decimation process see the section Low-pass filter test.
The program for reading the resulting binary files is called follow.filter.f (a modification of follow.f).
To simulate the Poisson distribution of the reorientation times (or the disruption times): if you use a sample, say, of 1000 bodies and a time step, say, of 0.1 Myr, with a reorientation (disruption) time of 3.3 (20) Myr it's enough that every time step you reorient (disrupt) 1000/33 ~ 30 (1000/2000 = 5) bodies choosing them completely at random. (forwarded email from Paolo Farinella)
 |
 |
 |
 |
 |
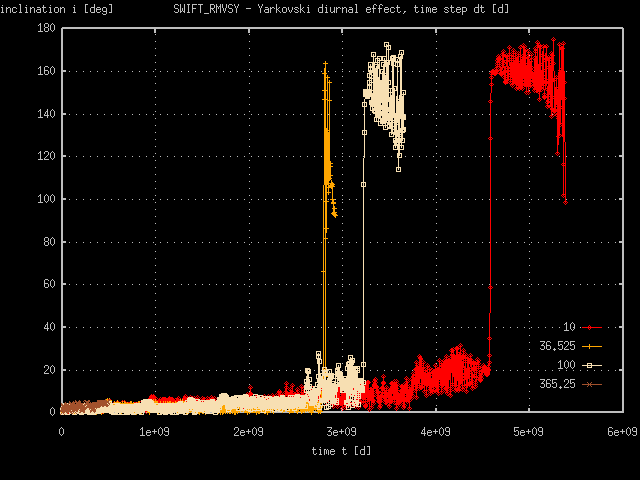 |
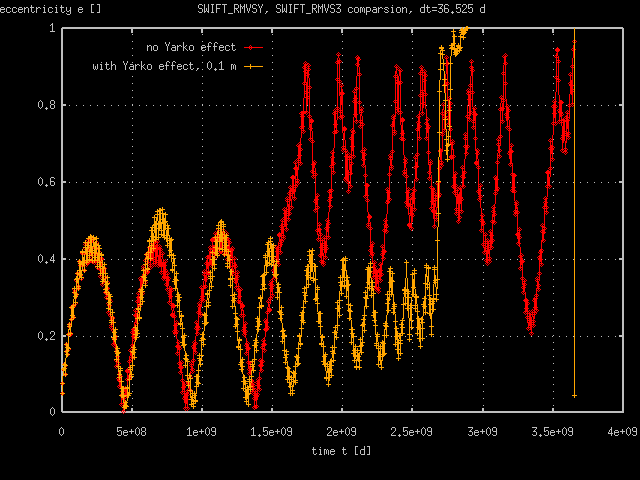
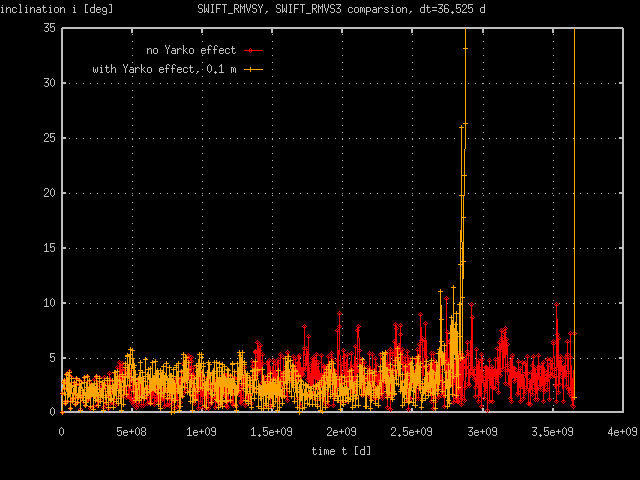
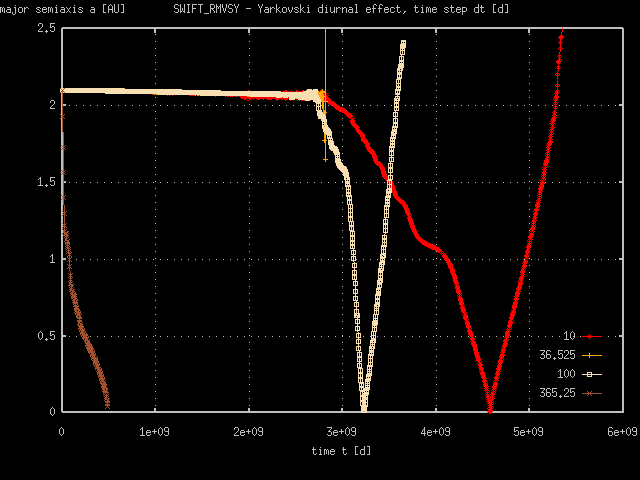
Summary: Notice that time step 365.25 d is too long - the major semiaxis falls to zero value very rapidly, while eccentricity is lower than 0.6. Time steps 100 d, 36.525 d, 10 d are in a good agreement until the eccentricity reaches values almost equal to the unity. In this state the thermal effect are set into work and major semiaxis starts to decreace in rates of order 0.1 AU · My-1. The time step shoud be shorten, to get a better agreenment in high eccentricity states. Well, may be, we need not to continue in the calculation, when the fragment becomes a sungrazer (e > 0.998 with a = 2 AU).
Note: This method is very stable for dt = 365.25 d in 1+1 body problem. The orbital elements of zero mass body were constant upto single precision after 1 My integration.