
The purpose of this page is to identify possible new members of the Eos family associated with the z1 = g+s-g6 -s6 resonance. The Yarko simulations indicate, that an excess of asteroids in this resonance may be directly linked to the existence of the semimajor axis mobility in the family (thus the Yarkovsky effect itself). This is especially true at lower inclinations, where the objects ``sliding along this resonance'' may form a sort of jet out of the family. Our ultimate goal is to prove existence of this structure in the Eos family. Note that at high inclinations such ``fugitives'' are much less likely, since they should typically encounter the J9/4 resonance and thus be ejected along this powerful mean motion resonance.
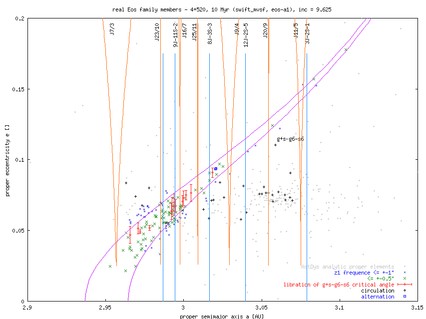
Let us first see the ``proper element facts'' related to the Eos family. Since the peculiar character of the z1 resonance (dependence on all proper elements), we follow the same method as in the main page devoted to the Yarko simulations of the asteroid families. In particular, we plot position of the proper a vs e (Milani and Knezevic analytic elements) in the thin ``slabs'' of the proper inclination (i.e. in each frame all asteroids have their proper inclination within 0.125° around the central value indicated in the title). So think in terms of cutting the family in the 3D proper element space in thin slices of the proper inclination. The following animation shows a sequence of such frames starting from the 8.625° to 11.875° in the proper inclination. First what is the meaning of different symbols:
So here we go with the animation (position of several mean motion resonances is indicated by the orange and blue vertical lines; approximate borders of the z1 resonance is given by the magenta lines)...
We were mostly amazed by the three frames with objects of the mean proper inclinations 9.375°, 9.625° and 9.875° (at smaller inclinations it is unclear whether the background objects would not dominate). Here they are once again
 |
 |
 |
It is somewhat suggestive that the green crosses (resonant objects) are in slight overabundance with respect to the surrounding area and might be the ``jet structure of the Eos family''. We thus propose to observe preferentially these asteroids with ``hope'' that they will be spectroscopically identified as the Eos members. To that end we have prepared a list of these objects and put them on top of this page.
Selection criteria. The goal of our study - i.e. proving existence of the Eos fugitives along the z1 resonance - made us to adopt some selection among all resonant objects in the Eos family zone. Notably, we discarded objects from the very-low inclinations frames, since these may be dominated by the background population of asteroids. Moreover, it is not our intention to observe the asteroids that are ``deep'' in the zone of the Eos family (even though they are in the z1 resonance). We thus selected asteroids with e < 0.05 (at the bottom of the family) and i = (9.25°; 10.0°) and obtained 71 bodies. A full list of these objects is given in the second item on top of the page. Next we also selected a subset of these asteroids, that are observable later this year (from Oct-Dec) - just in case somebody could offer some spare time in his observation program and devote it to ``our'' asteroids. There is 28 of such asteroids and their list is the very fist item on this page.
You may also see the target subgroup below the blue line on the following plot.
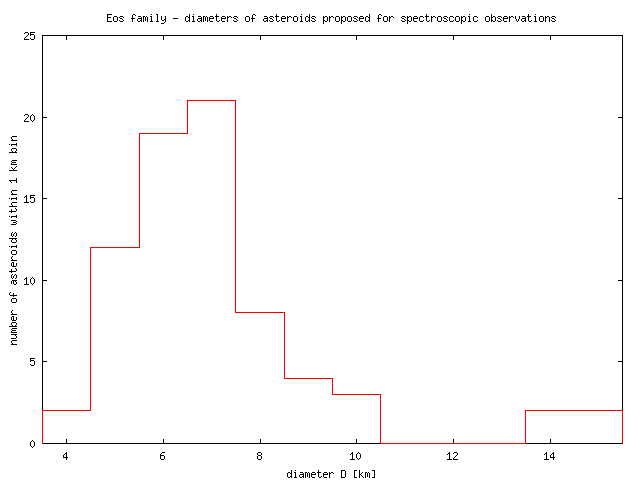
Mean albedo and diameters. The mean value of albedo of Eos family members is AEos = 0.12, as inferred from known diameters (Tholen's data, provided to us by B. Bottke) and absolute magnitudes (taken from astorb.dat catalogue). You can see the corresponding albedo data file, sorted according to albedo value, and also histogram plot.
Since we are interested to know if the Yarkovsky effect might have transported these asteroids along the z1 resonance toward their present location, we were curious to know their sizes. Obviously, too large bodies among this group of asteroids would be an obstacle for our interpretation. Based on the albedo analysis given above, we estimated diameters of above selected 71 asteroids in the z1 resonance. They span a range of 5 to 15 km, with the largest object being (8340) Mumma with D ~ 14.1 km. All other objects have D < 10 km and small asteroids (D ~ 6 km) dominate (see also histogram below). Note that these are really small asteroids which is good for the Yarkovsky scenario (there are at least 200 larger members of Eos known today).
The maximum diurnal Yarkovsky drift for these bodies is of the order (1-3) × 10-5 AU/Myr. The estimated time to drift ~ 0.03 AU (from the family center toward their typical present positions) is thus of the order of 1.5-3 Gyr; this is a fairly reasonable value that may match the family age.
Dynamical link of the candidate asteroids to the Eos family. The classical family-identification analysis has been done years ago. All candidate asteroids that we are discussing on this page were discovered later, and thus could not be initially included in the identification analysis of the Eos family. Here we are speaking about the purely dynamical identification, based on the asteroid positions in the proper element space. We have thus repeated such identification analysis based on the hierarchical clustering method (HCM; Zappala et al 1994) using (i) updated database of the proper elements (~61000 numbered and multiopposition asteroids in the AstDys files), and (ii) using the program in C written by David Nesvorny. From the two free parameters of the method, we chose the metrics in the proper element space as Zappala et al. (1994). We are thus left with the second free parameter, notably the velocity cut-off that halts the identification chain. In what follows, we test the level at which our candidate objects become members of the Eos family when using the HCM.
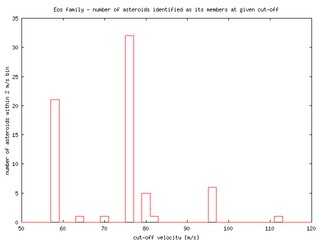
We found, that 68 candidate objects get identified as the Eos members at the ~110 m/s cut-off (only 3 objects of our candidate sample were not identified even at he 120 m/s level). The left plot below side shows distribution of the velocity cut-offs, at which our candidate asteroids get identified with the Eos family. As it might be expected, the distribution is not homogeneous, but the candidate asteroids get identified "in groups". The graphs indicates, that there are two significant groups, one at cut-off ~ 58 m/s and another at ~ 76-80 m/s. The first group might be considered still inside the family, but the second is at its margin (given the high velocity level) -- this, however, does not contradict our idea because remember that we are seeking for possible escapers (or escaping objects) from the family. Here you may get a complete list of our 71 candidate asteroids with the cut-off levels at which they fall in the Eos family.
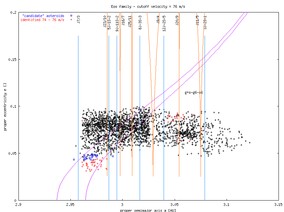
For interest, you may also trace how the Eos family "grows" with increasing the HCM-identification treshold velocity in the following animation (here again we used the AstDys database with ~61000 numbered and multiopposition asteroids). At each 2m/s-step the newly aquired objects are shown in red, and our candidate asteroids are then depicted by blue squares (note the two clusters at 58 and 76-80 m/s). If you do not like the animation, you may see the individual frames by clicking on the right figure below.
 |
 |
Bus' spectroscopic catalogue. We checked the SMASS catalogue by Bus (1999), but NONE of above proposed asteroids have been spectroscopically observed. Here is what the current SMASS data contain in this zone of the asteroid belt.
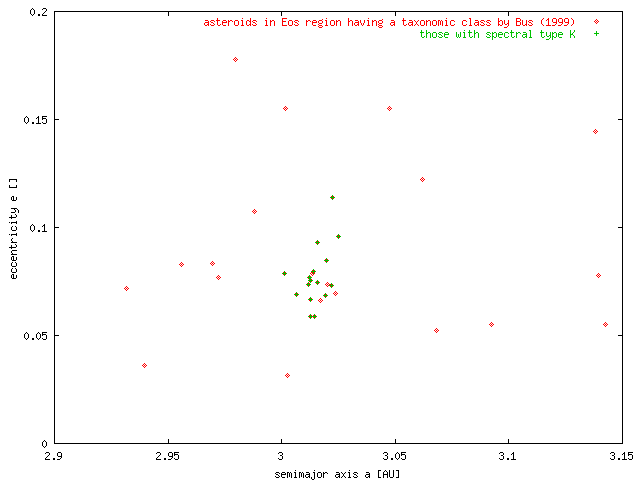
Rem. The two bodies with eccentricities e < 0.05 are not located within the z1 resonance borders - they both have quite different inclination.
Photometric data. We also looked for the data at the CALL site (maintained by A. Harris). Unfortunately, none of "our" asteroids was photometrically observed (and thus we do not know anything either about their rotation periods or positions of poles).
As a long-term goal, it would be useful to have informations about obliquities of our "candidate" asteroids, because we need "most (if not all)" of them drifting to the lower semimajor axes (ie. to the left).