
For the S-type families (Flora, Maria, Eos, Eunomia and Koronis) we assumed a low-conductive regolith of the thermal conductivity K=0.001 W/m/K (the thermal capacity is 680 J/kg/K and the surface density is 1.5 g/cm^3). These values match reasonably well those of the lunar (and Phobos) surface, but - what more important - are consistent with observations of Eros by Near (???) and small asteroids by ISO (Muller and Lagerros 1999). Bond albedo 0.1 and thermal emissivity 0.95, fits also their mean for S-type asteroids. The assumed value of the bulk density - 2.5 g/cm^3 - corresponds to S-types.
For the C-type families (Themis and Dora) we also assumed low surface conductivity of K=0.01 W/m/K; here the somewhat higher value than given above for S-types should correspond to ice components in the surface regolith (ice is a good conductor and increases the effective value of K). Here the direct observational evidence is virtually absent, except of models of cometary activity. We may thus admit somewhat larger uncertainty in modeling the Yarkovsky effect for the C-type families. Bond albedo 0.02 and thermal emissivity 0.95, fits also their mean for S-type asteroids. The assumed lower value of the bulk density - 1.3 g/cm^3 - should follow from icy components and high porosity.
It may be worth to point out that despite of persisting uncertainty in the Yarkovsky effect modeling for individual orbits, the corresponding error of the statistical quantities (like the growth of the family dispersion in a) may be much smaller. Though we do not have an exact prove for this statement, this is a general wisdom from other studies.
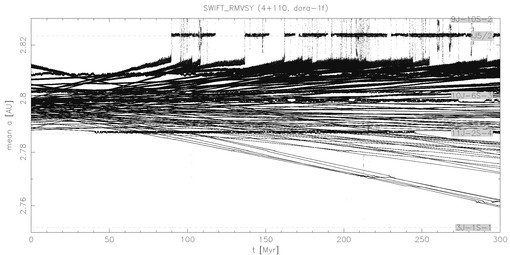
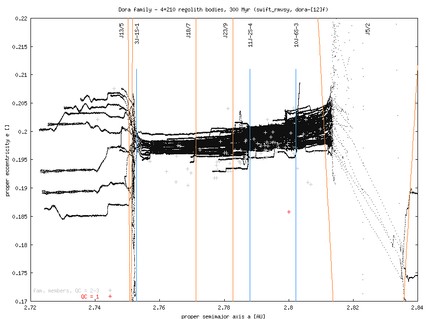
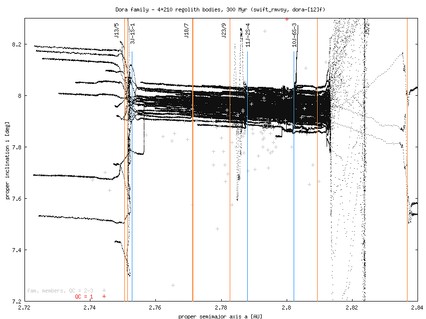
Dora: integration time span 300 Myr, *-1 run contains asteroids of sizes in the range 4-19 km, while *-2 run contains asteroids of sizes from 4 km downto 2km (smallest objects in each of the simulations have D=2 km). Here is what Bill B wrote about the data of this family (with a plot in proper-element space). Dora is specific by the closeby J5/2 resonance. The four km-sized object in the run dora-2f, that crossed the J5/2 resonance, would likely be ejected by close encounters with inner planets. About 25% of small asteroids (and fast drifting) asteroids in dora-2f escaped through the J5/2 resonance. At the other side of the family, asteroids that reach the 3J-1S-1 resonance (at ~2.75 AU) are significantly scattered in eccentricity, so they would not be identified as family members.
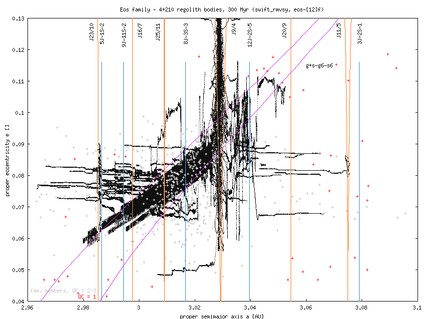
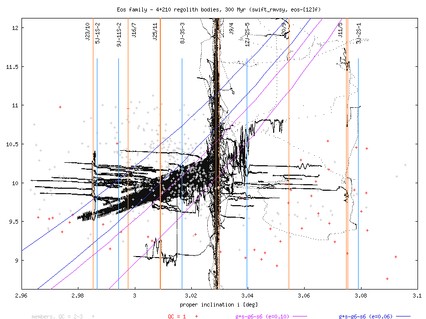
Eos: integration time span 300 Myr, *-1 run contains asteroids of sizes in the range 4.3-65 km, while *-2 run contains asteroids of sizes from 4.3 km downto 2km. Here is what Bill B wrote about the data of this family (with two plots in proper(a) vs proper(e) space: R>15 km and 15 km>R>5 km). The strong mean motion resonance J9/4 is a significant feature in this family, and a number of asteroids may leake out by increasing its eccentricity. Another, but more subtle resonance, that may affect the long term dynamical evolution in this family is the secular resonance g+s-g6-s6. This cannot be noticed in the a(t) plot, but will clearly appear in the proper element space. Milani and Knezevic (1992) briefly analysed Eos members as regard to their possible location in this resonance, but limited computer power prevented them to perform a complete study (they did only 10Myr runs for several asteroids but definitely not all Eos members). Looking at Bill B' data for 5-15 km sized asteroids (a-e proper element plane), one may be tempted to "believe" that a non-negligible fraction of the Eos family members are located/close to this secular resonance, but it may be just an "optical" illusion. To be more precise at this point, we ran orbital evolution (without Yark-effect) of 520 Eos members (all currently known members according to Cellino's list) for something like 30 Myr. This should be enough to determine which of the asteroids reside in this peculiar resonance (our preliminary look at the data say that there are some 31 percent of Eos members interact with this secular resonance). We hope that this might be an interesting test to trace footprints of the ongoing mobility in the Eos family, since we clearly see that Yark-moving orbits get ``stick for a long time'' to this resonance. First results can be found below.
Additionally, I guess that David N did check that several larger members of the Eos family are clustered in the 8J-3S-3 three-body resonance. Indeed, we checked that several of the slowly drifting asteroids in eos-1f get temporarily captured in this resonance. Above the J9/4 resonance the motion seems to be quite irregular (other resonances?), which may add to the reason why we see so few Eos objects there.
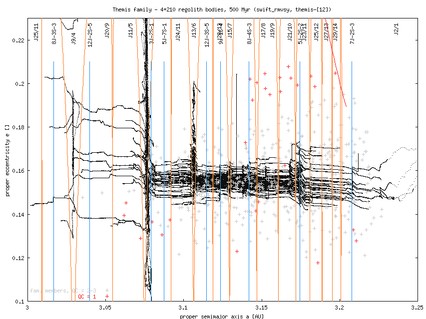
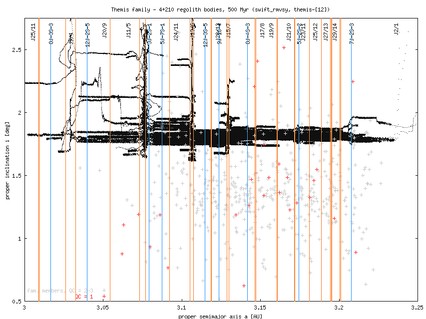
Themis: integration time span 500 Myr, *-1 run contains asteroids of sizes in the range 4.4-110 km, while *-2 run contains asteroids of sizes from 4.4 km downto 2km. Here is what Bill B wrote about the data of this family (with two plots in proper(a) vs proper(e) space: R>20 km, 20 km >R>10 km and 5 km>R>10 km). The family is very broad and covers a portion of the outer belt with many miniresonances. Obviously, the principal resonance at the outer edge is J2/1. We centered the initial data around ~3.13 AU, so that only few (4) of the smallest asteroids reached the J2/1 resonance within the 500 Myr limit. All of these were ejected. We obviously keep track of the puzzling group of Zhongguos in our plans and we intend to perform an additional simulation by placing a significant number of test particles at the bottom part of the J2/1 resonances and let them drifting up in semimajor axis. Our simulation indicates that closeby (at larger eccentricity even overlapped) resonances 3J-2S-1 and J11/5 at the bottom part of the family are very efficient in dispersing bodies in the proper(a)-proper(e) plane, so that those that crossed this area may not be identified as the family members. Quite powerful are also the first-order resonance 5J-2S-2 (at ~3.173 AU) and J13/6 (at ~3.105 AU). There are also weaker resonances (7J-2S-3, J15/7, J17/8, etc.) with still large enough effect to be noticed in our simulation. As it will be seen below, these miniresonances are quite efficient in dispersing the family in eccentricity, which is "good" since Themis has also considerable extension in e.
See also alternative images (with different semimajor axis range).
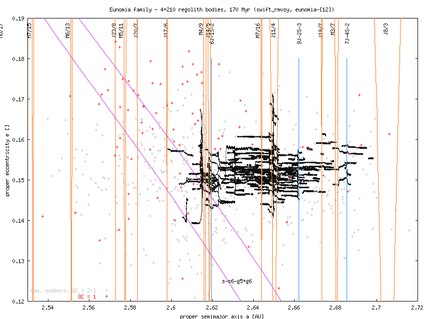
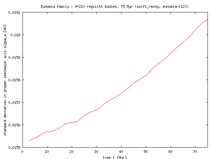
Eunomia: here we give only preliminary figures of approximately 75 Myr integration (we plan to finish this integration to ~300 Myr as for the other families). The sizes of asteroids range from 45 km to 4 km in *-1 run and from 3 km to 2 km in *-2 run.
See Bill B. text and his (a, e) plot concerning this family. The evolution of Eunomia spanning 175 Myr was also calculated by D. Nesvorny and A. Morbidelli (with previous version of on-line filter :-(
Remarkable mean motion resonances in the Eunomia region seem to be J11/4 with Jupiter and weaker 3-body resonances 6J-1S-2, 9J-2S-3, 7J-4S-2. We also noted the role of s-s6-g5+g6 secular resonance (see below for examples).
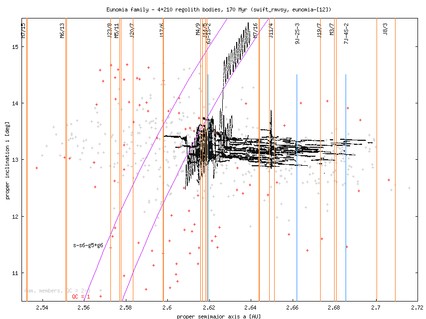
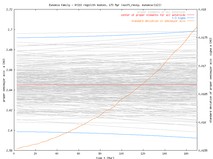
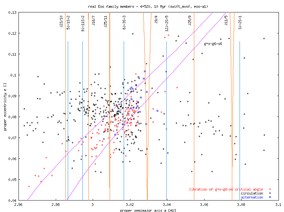
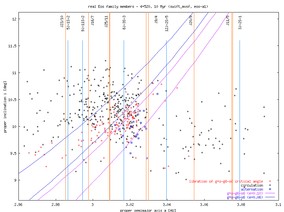
The observed family members are superimposed over the simulation by crosses; data from Bill Bottke coincide well with those indicated by those produced by A Cellino. For this moment we used only the numbered members with numbers smaller than ~5400 (hope to extend to all currently numbered members soon). The grey crosses are fair members (Cellino's quality parameter 2 or 3), while red crosses are tentative members (Cellino's quality parameter 1).
In the right hand side plots you may compare the observed family (the orange cross then indicates the larges member of the family) with the initial conditions of our simulation: (i) osculating initial elements, and (ii) proper elements computed from the first 5 Myr window. The first 5 Myr evolution in the family typically does not change the elements much; the exception id Eos, where you may already notice the influence of the g+s-g6-s6 and g+s-g5-s7 resonances. Notice the typically large difference between the osculating and proper eccentricities, which is due to forced oscillations of the osculating elements due to planetary perturbations. The ``initial'' proper eccentricities are typically well-positioned in the observed family, with only a small misfit for Dora and little larger misfit for Koronis. Perhaps, we were not enough careful when producing the initial conditions, but I believe that this shift is not essential for our conclusions. What really matters is how the family disperses in time.
 |
|
 |
|
 |
|
 |
|
| not yet available |
As above, the observed numbered (<5400) family members are superimposed with symbols (grey/red crosses depending on the quality factor of the identification) over the numerical simulation.
The right hand side plot indicate comparision of the family (in the appropriate proper-element projection), the initial osculating elements and the proper elements computed from the first 5 Myr of our simulation. Things are ``reasonably'' good except from Themis (see also below, where we plot the histograms of the proper element distribution). Anybody has an idea? small-inclination problem? after all the osculating elements typically oscillate between 0 - 3.5 degrees.
 |
|
 |
|
 |
|
 |
|
| not yet available |
Notice, for instance, how the Themis family becomes more dispersed in eccentricity for a > 3.15 AU due to interaction of the Yarkovsky drifting orbits with miniresonances. The real data of the family indicate that this is true; moreover, a number of real family members located in the 5J-2S-2 (and widely spread in proper eccentricity) are an indirect hint for capturing of the Yarkovsky-drifting orbits in this resonance (see the last slide of our simulation - at 500 Myr - with 8 particles captured in this resonance).
The animations above show one more feature: sizes of the asteroids (estimated), or TPs (modelled), are indicated by the size of the symbols (circles). Dora looks good and the family may be something like twice old than the timespan of our simulation (~ 0.5-0.8 Gyr say). As expected, Themis (for instance) is a more difficult case. Please do not be ``frustrated from scratch'' by seeing that only small (~ km-size) particles disperse enough in our simulation, while the observed family (gold symbols) indicate that also larger asteroids are well dispersed between ~3.07 - 3.22 AU. Take into account that the timespan of our simulation (0.5 Gyr) may be just a fraction of the family age. If the family were 2.5 Gyr old (i.e. 5 times more than our simulation) then ``multiply'' the size of the smallest TPs in our simualtion by this factor 5 (since Yark-mobility is inversely proportional to the size). We may thus get objects of the ~5 - 7.5 km radius (the smallest observed) well dispersed throughout the whole family in the 2.5 Gyr age. This conclusion is supported by the Monte-Carlo simulations discussed at the bottom of this page.
The distributions are compared to the identified members (yellow curve); here we used data files by Cellino (provided to us by Morby) but later we would like to compare it also with data files of Bill B. Number of observed asteroids in each family (e.g. from 78 upto 550 in Cellino's files) is normalized to 210, to be able to directly compare with our simulation.
A complete list of histograms is N(a), N(e), N(i) is available.
| family | semimajor axis N(a) | eccentricity N(e) | inclination N(i) |
| Dora | 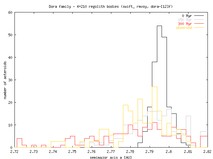 |
 |
 |
| Eos |  |
 |
 |
| Themis |  |
 |
 |
2DO: comments on distributions of a, e, i of all other families.
Themis. You may notice that in eccentricity our simulation still "lags behind" the true family dispersion, but we should take into account that 500 Myr may represent only a 15-50% fraction of the family age (so that further dispersion in the modelled data may be expected).
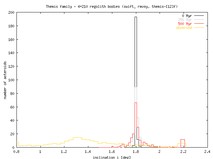
Themis inclinations. We are a bit concerned about the Themis distribution of inclinations and its comparison with the data from A. Cellino's file. Though the eccentricity dispersion might eventually fit (after extrapolating evolution, doubling or tripling the family age), inclinations seems to present a problem. The family data have much broader distribution in i with a shallow maximum at ~ 1.3 degrees. This is in contrast with Themis proper inclination of 1.08 degrees (rather off the peak of the distribution); the miniresonances seem to apreciably affect the proper eccentricities, but much less the inclinations (see the above plotted evolution of the family in the proper a - proper i) projection). Anybody has some idea?
Additional informations on this issue: (i) a typical oscilation of osculating inclination is more than 3° (with mean value above 1.5°, which corresponds to the center of "our" histogram) - as could be seen in i(t) plot for one particular particle. (ii) The initial osculating inclination of Themis - parent body was set around 0.8° - see list of initial osculating elements (a,e,I,...) of themis-1 run and this (a, i) plot with comparison of initial osculating and proper elements with the real family. The fact that our proper inclination is centered around 1.8° means probably that we were not very careful in chossing the initial elements of the asteroids (they were ``too low in the inclination oscillation cycle''; ?). (iii) You can also compare proper elements from A. Cellino data-file with those by Milani and Knezevic (downloaded from AstDys) - they agree very well. (By the way - note a clear "trace" of J11/5 resonance at approx. 3.75 AU visible on this image - very few asteroids were identified as family members "behind" its border.)
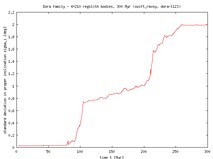
The initial and final standard deviations of the distribution in semimajor axes are as follows: Dora 0.005 AU and 0.025 AU, Eos 0.012 AU and 0.018 AU (both after 300 Myr), Themis 0.012 AU and 0.042 AU (after 500 Myr). As expected, in all cases the family dispersion increases (after a certain time the increase is nearly linear in time). Obviously, this is the Yarkovsky feature. As it will be discussed below, this trend should stop in reality because of collisional evolution in the family.
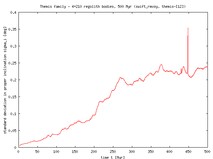
The corresponding values of dispersion for the eccentricity and inclination are also shown in the figures collected in the following table. Here the evolution is less reguliar, especially in the the case of Dora where only a few of miniresonances are located. The best seen is for Themis, where (on the contrary) a large number of miniresonances are located and are able to temporarily alter proper eccentricity or inclination. On contrary to the semimajor axis, the quasilinear trend here should be affected less by the collisional evolution of the family. As before, the fluctuations correspond to fast ejections of particles from the simulation.
To compute the standard deviation of the family dispersion, we should obviously ``somehow'' eliminate asteroids that leak out fo the family through principal resonances (e.g. J5/2 for Dora), since these are no more family members and would artificialy increase the computed dispersion. Ideally, we might contrast the family with a background population in this part of the asteroid belt and check at each timestep which of our integrated asteroids would be still identified as the family members. For this moment, we chose a somewhat simpler option and we use the following algorithm (applied to each element): (i) compute center of the family, (ii) compute standard deviation of the distribution and eliminate all asteroids that exceed 3-sigma distance from the center, (iii) iterate back to (i) until no more asteroids are eliminated by the procedure. We then report the final value of the family-center and standard deviation in the corresponding element.
The first column in the table shows evolution of the proper semimajor axis as a function of time in our simulations, computed center of the family (red curve), 3-sigma range (blue curves) and the standard deviation (orange curve and the right ordinate). You may see, that e.g. for Themis we have a few asteroids that do drift so fast that they escape from the 3-sigma range from the center and are ``eliminated'' from the family. The work is done similarly for the eccentricity and inclination.
| family | a(t) plot | standard deviation in semimajor axis | ... eccentricity | ... inclination |
| Dora |  |
 |
 |
 |
| Eos |  |
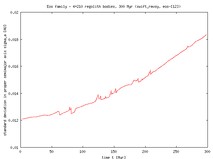 |
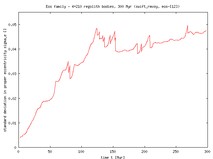 |
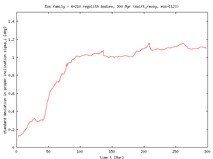 |
| Themis |  |
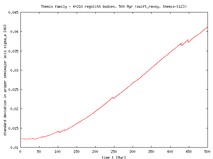 |
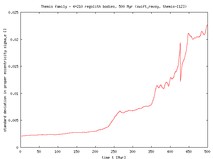 |
 |
| Eunomia (75 Myr) |
 |
 |
 |
 |
Resonance crossing analysis. You may also get a more direct feeling how the ``weak'' resonaces affect the mean semimajor axis by going here; for selected resonances (such as J13/5 (3J-1S-1), J9/4, J23/10 (5J-1S-2), J11/5 (3J-2S-1), J13/6, etc.) we zoom at their close vicinity. We also analyse in a quantitative manner the resonant captures/jumping for those resonance, that were encountered with ``statistically'' enough particles.
Critical angles. We produced plots for three particular test particles from eos-2f run: no. 1 - proper (a, e), a(t), e(t), g+s-g6-s6 (t) for 0-300 Myr; notice the first ~ 140 Myr phase, when the particle was ``sliding'' along this secular resonance (as a result of the Yark-mobility in the semimajor axis) until it hit the zone of J9/4 resonance and later was scattered out of the family; no. 3 - proper (a, e), e(t), sin i(t), g+s-g6-s6 (t), g+s-g5-s7 (t) (you also can view the evolution of node, peri and varpi for this asteroid and also for Jupiter and Saturn); and no. 62 - proper (a, e), (a, sin i), e(t), g+s-g6-s6 (t), g+s-g5-s7 (t); this is again an interesting case of a TP, that has been ejected from the g+s-g6-s6 resonance at ~ 125 Myr, likely as a result of the interaction with the 5J-1S-2 multiple resonance, but later again reach the secular resonance.
We observe strong perturbations of e and i, evidently driven by the secular resonance - TPs "slide" exactly along expected resonant borders, and also corresponding librations of critical angles with the same periods. The g and s frequences for planets were taken from Milani and Knezevic (1997) software secre8. (The longitudes of nodes do not circulate in our ecliptic reference frame - David Nesvorny comment.)
 |
 |
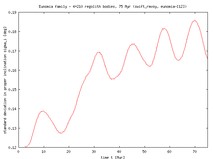
For purpose of this test, we integrated 520 known members of the Eos family (data from the Cellino's file; initial data from astrob.dat) for 25 Myr. Yarko-effect was not taken into account here, so that we could you the original version of swift; inner planets were not integrated. We looked at the results after 18Myr of this simulations have been completed and produced the graph on right. You can see Eos as projected on the proper (a,e) plane; 162 out of 520 asteroids interact with the g+s-g6-s6 resonance (ie. 31 %). We can say that because we individually looked at the evolution of the g+s-g6-s6 resonant angles. In particular, for asteroids indicated by red diamonds the corresponding resonant angle permanently librates, for asteroids denoted by blue squares we see alternation between librations and circulations (since they lie at the border of this resonance or some of them are in J9/4 resonance that temporarily drives them to this secular resonance), and the black crosses are out of the g+s-g6-s6 resonance. We also indicate a rough position of this resonance as given by the semianalytic approach by Milani and Knezevic; note, however, that this resonance is a really 3D structure in the proper element space (unlike the mean motion resonances); the indicated position corresponds to the mean inclination in the family, but we can also see some ``red-asteroids'' ouside, meaning that their inclination does not fit the family-mean (and vice-versa: there a few black crosses where we would expect the resonant asteroids, but the point is that their inclination is ``out''). Clearly, the bulk of the resonant asteroids is where we expect them and there is also the weak-feeling of a stream of asteroids at the left-bottom part. Obviously, we should not exaggerate, but we anyway found this test interesting. We would be happy to hear suggestions what more we could do?
A drawback of the previous plots stems from the fact, that we have projected all the Eos members onto a single planes of proper(a) vs. proper(e) or proper(a) vs. proper(I). This fact ``messed'' the 3D structures in the family. Note, that this is not important for the mean motion resonances, that are basically identified by the proper(a) value (and only weakly open with the increasing value of the proper(e) or proper(I)). However, the secular resonances, like the one we are studying here, are fundamentally 3D structures in the space of proper elements. In the following animation and plots we cut the Eos family onto slices in proper inclination (each of the 0.25 degrees thick) and show the data for each of the slices separately. This helps understanding the 3D aspects of the Eos structure. Few immediate conclusions: in each slice we plot (i) the Eos members and by red symbols we point out those that were found in the resonance (through libration of the corresponding resonance angle), and (ii) the approximate position of the resonance by using the software by Milani and Knezevic. We may observe, that the way how the ``red asteroids'' fit to the expected location of the resonance is perfect. More importantly, this analysis helps to really see how the Eos family is structed in the proper element space. It is nothing like a triaxial ellipsoid. In the low-inclination ``frames'' we may notice a ``jet'' of asteroids with low values of proper(a) and proper(e), a structure that may be formed by the resonance.
In our Yarko-simulation we do see how the TPs slide along this resonance. For sake of a direct comparison, we have plotted the final state of our 300 Myr evolution of the Eos family with the Yarkovsky effect using the same technique (i.e. in the frames of quasi-constant proper inclination). Here you can see the corresponding animation or the plots. Note, that 300 Myr may not be enough timescale to reach the position of the outermost asteroids in the zone of the z1 resonance, but we are able to reproduce the general features of the Eos structure here.
A still more involved analysis is summarized here:
Two more integrations were performed to check the behavior of z1 critical angle of each "candidate" asteroid for spectroscopic observation. (These are NOT mentioned on previous "public" spectroscopy web page!)
First we selected 56 bodies (eos-a2 run) with frequency z1 < 0.5 "/Myr: see their evolution of critical angle and eccentricity, list of non-librating and alternating (+) bodies (they were NOT dicarded from our list of candidates) and 3 slices in inclination (including also positions of largest asteroid (8340) Mumma and asteroids from eos-a3 run - see below).
In the next set of 20 asteroids (eos-a3) with 0.5 "/Myr < z1 < 1.0 "/Myr most of them also librate, surprisingly. Look at: critical angles and eccentricities and list of non-librating bodies (these WERE dicarded from the candidate list).
We are preparing (a, e) plots of the family for different slices of the ``proper'' inclination; check here later for the corresponding animation or the individual figures.
The integration of Koronis family is performed on a Windows NT computer, TPs sometimes perform unexpected jumps in semimajor axis during frequent restars of the runs.
See also SWRI web for new results on Flora, Eunomia, Maria and Koronis families: http://www.boulder.swri.edu/~davidn/yarko/yarko.html, http://www.boulder.swri.edu/~bottke/Animation/.
To recall, the principal "free parameters" of the simulation are: (i) the age of the family, (ii) the f_KE factor that tunes initial compactness of the family (in semimajor axes), (iii) the empirical factors cf1 and cf2 of the axis-reorientation and disruption timescale. We may also test sensitivity of the results on changing the steepness q of the initial size distribution.
Which parameters we store in course and at the end of the simulation?
In the first figure you see initial (green) and final (black) distribution of the modeled Themis family in the above indicated four size bins. You may clearly see how the family expanded in course of time. Notice a decrease at ~ 3.07 AU (first two bins); this is my elementary attempt to include the influence of the J11/5 and 3J-2S-1 resonances. When the drifting objects spand longer time than ~ 50 Myr in the zone of these two resonances, I eject them from the simulation. Obviously, I would be happy for any suggestions how to improve my model in this respect. If Bill B would send me his data file of Themis I might plot here a comparison with the observed Themis a-distribution.
From the data above, I may compute how the standard deviation of the semimajor-axes distribution changes in time; here is the corresponding plot. In black you see the modeled family, green are the data from Bill B for the current family (as I discussed above, the real sigma(a) in the largest bin - 15-20 km - may be lower according to data file of A Cellino). Notice the expected features of the solution. The smallest bodies move fast so that their sigma(a) increases significantly in the first phase of the simulation. However, these bodies have also the shortest lifetime, so that they become to disappear from the family first (also falling in the J2/1 resonance). This produces flatenning of the sigma(a) "dynamics" in the smallest size bin for epochs later than ~ 0.5 Gyr. Notice, that this is by chance maximum time of our numerical simulation above. Small bump in the sigma(a) of the smallest size bin at ~ 1.75 Gyr is caused by disruption of one of the family large members (~100 km size in my simulation), that was obviously located near the center of the family. Dynamics of sigma(a) at larger size-bins is slower, but more steady.
Finally, let us have a look at the size distribution of the family members. The following plot shows my initial distribution (green), final distribution affected uniquely by the collisional evolution of the family (blue), "modeled" distribution (red), where I have applied some guessed completeness-factors in different size-bins, and the observed (black) size distribution of Themis members (here I use data file by A Cellino). The difference between green and blue curves indicates that family looses small members faster than replenishes from break-ups of larger members, so that the steepness of the distribution get shallower at small sizes. These small sizes are then affected by observational effect of our incomplete knowledge of the family members (blue -> red curves). Here I have assumed the following ad hoc completeness factor, by which I have multiplied the modeled final distribution. I would be very happy, if somebody could tell me more reasonable numbers. At the moment I looked at Fig. 5 of Jedicke and Metcalfe (1998), where they compare Spacewatch debiased population with observations performed by Palomar Leiden Survey; well, you see that this is already a sort of hybrid information. The magnitude bins in this figure were recomputed to the size bins using an approximate formula D ~ 5900 10^{-0.2 H} (in km); obviously I took take from the 3.0-3.5 AU range. Obviously, we cannot get the really good fit of the observed size distribution (black curve), since we do not have the truly self-consistent collisional model. For instance, I would believe that the hump at ~ 80-90 km sizes might have to do with changing the regime by which the bodies "keep together" - gravity vs. molecular cohesion - and this rules their strengthness with respect to disruptions. Things like that should be modeled by a dedicated study. I am basically satisfied, that we could obtain something "reasonable" without putting in some really crazy factors. Suggestions?
My next plan is to see what happens if I force the spin axes of the asteroids to evolve ``faster'', something that YORP suggests. One possibility would be to constrain the factor cf1 to be small, while still allowing cf2 large. However, this would not respect the right size dependence of the characteristic timescale of the YORP effect, which is much steeper than ~ \sqrt{R}, notably more like ~ R^2. Now, I am trying to work slowly on YORP with one of my students and we have some new findings, if compared to Dave Rubincam's Icarus paper, that I want to use here. First, let me explain what YORP does and what are the caveats of current modeling.
YORP secularly (``meaning periods longer than the orbital period'') changes (i) rotation rate and (ii) obliquity of the spin axis. The effect is nil for spherical bodies, but is generic for irregular shapes. The pioneering paper here in Rubincam (2000). Now you understand, that an infinite variety of shapes exist for asteroids (meteoroids) smaller than ~km across. See here for fun several well-determined shapes (axes are in kilometers):
 |
 |
| Golevka | Geographos |
 |
 |
| Castalia | 1998 KY26 |
 |
| Kleopatra |
These data were obtained using radar imaging by the Ostro's group at JPL. In our simulations we have used all these cases, plus a couple of others, but we have also generated ``synthetic'' objects by the Gaussian approach developed by Kari Muinonen (1996, 1998). Now one of the - expected - troubles with YORP is that there is no generic result of YORP: YORP evolution for Golevka is different from that of 1998 KY26 and this is still different from the YORP evolution of Kleopatra (you should understand ``the shape of ...'' since the linear dimensions of the object do not matter for the qualitative result). My impression is that this feeling is missing in Dave Rubincam's paper: e.g. rotation of any object of the Kleopatra shape will only be decelerated by YORP and never accerated, Golevka's obliquity will be asymptotically approaching some ~40 degrees, while obliquity of 1998 KY26 will approach 90 degrees, etc. There is, however, one major feature: if nothing than YORP is assumed for the spin axis evolution, the obliquity will be always assymptotically approaching some value (most often 0 degrees or 90 degrees, but any intermediate value is also possible) and at this terminate state of the obliquity evolution the rotation rate is in most cases (~ 95 percent of cases) decelerated. Hence the likely long-term YORP evolution is that the axis is slowly tilted to some asymptotic value; as soon as this is approached the rotation rate is decreased enough so that an impact will reorient the axis (and speed the rotation) and the cycle begins again. What matters mostly for our application, I believe, is the right estimate of the timescale on which this cycle occurs. With my another PhD student, David Capek, I have tried to estimate the statistically mean value of the YORP cycle duration (ie. starting from a random orientation and mean rotation period of 5hr till the YORP despuns the rotation to 50hr). We used a statistical sample of 1000 synthetic asteroids whose shapes were generated by the Gaussian random sphere technique of Muinonen (1996, 1998) and Muinonen and Lagerros (1998). For R=1 km Themis asteroid we got 60 Myr, rather short if compared with our 500 Myr simulation of Themis members with fixed orientation of the rotation axes. The factor 60 Myr is comparable to ~ 30 Myr we would got by appropriate scaling of the Dave Rubincam's (2000) result for Eros. This means that the YORP effect is slightly amplified for the Eros bean-like shape than in average for the Gaussian random sphere of Muinonen. For larger objects the 60-Myr factor scales as ~ R^2 (as I have mentioned above). So for R=3 km Themis asteroid the YORP timescale becomes ~ 540 Myr, larger than our simulation. Note, however, that there is an large uncertainty in the numerical values mentioned above, maybe up to factor 2. From what is summarized above, I propose the following approach (to start the thing): since the asymptotic obliquity is not generic (0 degrees with about the same likelihood as 90 degrees), just use the previous Poissonian statistical approach by keeping the spin axis fixed until a a condition of impact-reorientation is randomly satisfied. The reorientation timescale is, however, \tau_rot ~60 * R^2 Myr (with R in km). At small sizes this timescale is quite shorter that of the collisional reorientations; however, thanks to steep dependence on R the collisional reorientations begin to dominate for larger asteroids with size > 3 km (see above). We have thus started simulation of the Themis evolution with this zero-level modeling of YORP; only smallest 100 members are included in our simulation, since the larger objects should not presumably get any, or just one, reorientation within the 500 Myr period.
As a remark, I just note here a few caveats of the current YORP modeling (we again are working to remove them):
Anyway here, is what happens if I include in my Monte Carlo code the above mentioned, somewhat extreme (and obviously simplified), modeling of YORP-induced effects on the spin axes (random reorientations after the characteristic timescale \tau_rot ~60 * R^2 Myr.
You see, that the result is not ``that excellent as before'', since the frequent reorientations of small-size asteroids prevent them to diffuse due to Yarkovsky orbital effect very far from their initial positions (hence the ``bell-shaped'' distribution of the final semimajor axes in the 1-5 km size bin). The sigma(a) increases more slowly than before. Obviously, the real bonus of this simulation (apart from the fact that it should be ``more realistic'' since it includes anyway unavoidable YORP effect) should appear in the eccentricity and inclination distributions that are not modelled here. Namely, random wandering in the semimajor axis ``up and down'' due to axis reorientations should help to disperse the family in these other proper elements thanks to interactions with miniresonances. I am still running some more tests to see if could get a better result, so that we shall see more next week.
UNDER CONSTRUCTION (SEE LATER).