| inner | outer |
 |
 |
A model computation with Xitau:
This particular model has the following properties: monopole*, with the osculating periods P1 = 1.758099 d, P2 = 2.686243 d, mutual perturbations, massive moons, tides with Δt = 32.5 s, operating independently on the inner, outer moons, non-resonant orbits, corrected geometry, corrected equinox, convergence with subplex, χ2 = 273.
* It is equivalent to a more sophisticated multipole model (Broz et al. 2021, 2022), BUT with different osculating periods! Hereinafter, the precession of orbits is NOT apparent because the orbits are BOTH circular and equatorial. Secular multipole perturbations only contribute to the true longitudes λ1, λ2, BUT they do not change the geometry.
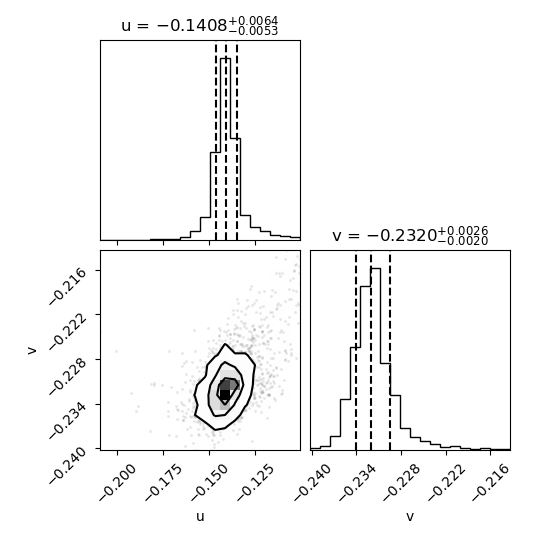
The sky-plane positions of the moons at the time of occultation Jan 21st 2023, 19:51 UTC = 2459966.327884 TDB:
u1 = -RA = -0.1408 +- 0.0064 arcsec v1 = +DE = -0.2320 +- 0.0026 arcsec u2 = -RA = 0.2861 +- 0.0030 arcsec v2 = +DE = 0.1401 +- 0.0060 arcsecwhere the uncertainties were determined by the MCMC:
inner outer
They are also indicated on the Figs. below (as "big residuals", from the centre to the position).
absolute astrometry (SKY) relative astrometry (SKY2) adaptive-optics silhouettes (AO)
A Jan 21st 2023 occultation computation with Xitau:
This computation has the following properties: (external) JPL ephemerides to interpolate the geocentric trajectory of the asteroid, (external) Gaia DR3 astrometric positions of the respective star, stellar proper motion, parallax, TDB→UT1 transformation, light time, precession, nutation, intersection with the WGS-84 ellipsoid, as well as rotation (GST). All of them affect the topocentric position substantially (>5 km).* The path (λ, φ) is available here: occultation.dat, occultation.kml. The KML file can be opened in Google Earth on the web; Projects, New project, Import KML file from computer.
* A (differential) gravitational deflection, or pole wander were not applied.
The uncertainty was propagated to λ, φ -- in Fig. below, scattered dots (from MCMC) were plotted for four locations (Portugal, Spain, France, Italy). The 1-sigma uncertainty is about 10 km (see the black bar, 20 km). For comparison, the model without tides is plotted in gray. The predicted difference between the models with and without tides is significant, however, this is related to the inner moon. For the outer moon, the respective uncertainty ellipses overlap.
Jan 21st 2023 detail Time stamps for JD-2459966 (TDB). Expected duration for the outer moon is about 0.20 second.
inner; in Tunisia outer; in France
Moreover, I verified all computations by the observed occultation of (216) Kleopatra, on Mar 12th 2015. The chords are exactly as in Herald et al. (2020), Fig. 8. Specifically, 3 are above the centre of mass, the remaining ones are below (or negative). The remaining issue was a difference 1.8 s in time (i.e., along track), which was not resolved. Possibly, the JPL Horizons ephemeris should be updated accordingly?
A comparison with Occult:
Corresponding maps from Occult are shown here for comparison.
Correct. Erroneous!
Conclusions: For Kleopatra, the computations with Xitau are fully compatible with Occult -- provided we use the JPL Horizons ephemeris for both of them. The shadow path Portugal--Spain--Sardinia--Italy is very favourable! It is probably better to be on the west, in order to have the star+asteroid high above horizon. The magnitudes are V = 11.2 mag (star), 11.4 mag (asteroid), 17.3-17.9 (moons); the resulting drop is about 0.85 mag. However, for the moons, the ephemeris in Occult/Miriade is outdated and the predicted positions are wrong, because the true periods are different. According to Xitau, the shadow path of the outer moon (Alexhelios) is in Spain--France--Italy. Croatia, etc. are perhaps too close to the limb. However, the observation of the inner moon (Cleoselene) in Morocco--Algeria--Tunisia is more important! Simply because it provides a very important constraint for the tidal evolution (see Broz et al. 2022). In particular, it would allow us to distinguish between the tides with and without the 3:2 mean-motion resonance between the moons. The difference should be clearly seen already in 2023 -- see Fig. B1 from Broz et al.