
We already analysed J9/4 resonance in the similar way. Note, that as in the case of the J9/4 analysis, we consider only the giant planets in our numerical simulation; the effect of the inner planets (on the resonance structure) is thus missing here.
Initial conditions: (all parameters expcept NTP, a, R are the same as in J9/4 integrations) NTP = 250; osculating elements: a = 2.963 - 2.965 AU, e = 0.03 - 0.12, sin i = 0.16 - 0.20 (in proper element space, the distribution is slightly more dispersed), random omega, Omega, and M;
Thermal parameters: radii (bins of 50 TP): 1.5, 3, 4.5, 6 and 7.5 km; bulk density 2500 km/m3, surface density 1500 km/m3, thermal conductivity 0.001 W/K/m, thermal capacity 680 W/kg/K, albedo 0.10, infrared emissivity 0.90, rotation periods 4 - 12 hr, obliquity 45° (ie. drifting outwards).
List of Figures and Tables:

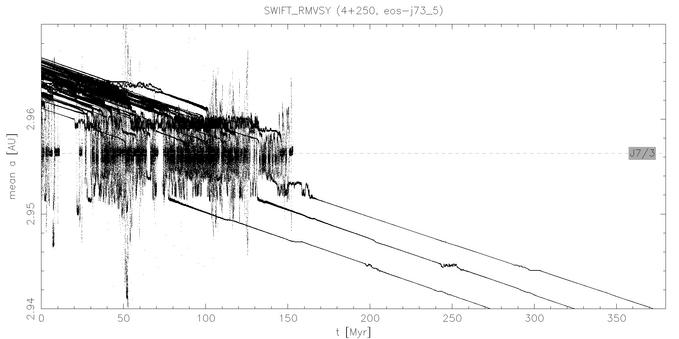
Figure 1 - Mean a(t) plot for R=1.5 km bodies. Only 3 out of 50 bodies (ie. < 10 %) crossed the J7/3. A capture in the resonance typically lasts less than 10 - 20 Myr, what is small in comparison with the time, which takes Yarkovsky drift to move a 1.5 km body by 0.005 - 0.01 AU (ie. approximate width of the J7/3 resonance). Thus we can say, we observe rather "jumps" than "captures"i, with respect to this time-span. (Btw. it is also less likely to observe "fugitives" of Eos family escaping through J7/3 resonance, because the asteroids may stay inside this resonance much shorter time than in J9/4 case - some of them almost several hundreds of Myrs.)
 |
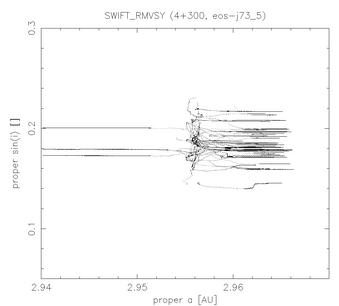 |
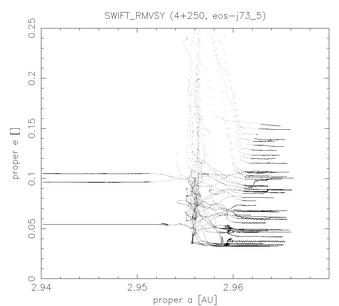
Figure 2 - Evolution of proper semimajor axis, eccentricity and sine of inclination for 50 TPs with R = 1.5 km (the same particles as in Figure 1). A few particles seem to be affected by a secular resonance (they exhibit periodic oscilations in e, i), but the (unknown) resonance does not increase/decrease significantly neither eccentricities nor inclinations. (The secular resonance is probably NOT z1, because its borders are quite "inclined" in (a, e) plane in region between 2.95 - 2.97 AU, while particles drift mainly "horizontally".)
| run | R / km | H / mag | t / Myr | NTP | initially above J7/3 | crossed (e < 0.14) | not yet entered | still inside | ratio below/crossed |
eos-j73_1 |
7.5 | 12.0 | 914 | 50 | 44 | 1 | 0 | 0 | 0.023 |
eos-j73_2 |
6.0 | 12.5 | 915 | 50 | 43 | 1 | 0 | 0 | 0.023 |
eos-j73_3 |
4.5 | 13.1 | 808 | 50 | 46 | 1 | 0 | 0 | 0.022 |
eos-j73_4 |
3.0 | 14.0 | 606 | 50 | 45 | 2 | 0 | 0 | 0.044 |
eos-j73_5 |
1.5 | 15.5 | 372 | 50 | 47 | 3 | 0 | 0 | 0.064 |
Table 1 - Summary of J7/3 resonance crossing analysis. For each run we list: radius R of TPs, corresponding absolute magnitude H (for mean albedo 0.125), time-span t covered by the numerical integration so far (most of the jobs are still running), total number NTP of particles in this run, number of TPs (NTP), which were initially above the border of J7/3 resonance, NTP crossing the resonance with e < 0.14 NTP, which did not enter the resonance yet, NTP staying in the resonance at the end of integration and finally ratio of bodies crossing on low e to all bodies entering the resonance (ie. the 7th column of the table divided by the 6th).

Figure 3 - Semimajor axes a and absolute magnitudes H of Eos family members (HCM at 100 m/s). The blue "envelope" denotes the maximum theoretical distance (in a), which asteroids (of given H, ie. size) could drift by the Yarkovsky effect (it corresponds to the approximate age of 2 Gyr; here we assume that the initial collisional distribution in a was small). It is empirically centered at 3.02 AU in order to get a good match of the bulk of the known family members with H between 10-14. More information about this figure is avaiable on the WWW page: Call for observations of the possible Eos interlopers.
At small values of a (below 2.96 AU) we cannot see almost any asteroids (even at this large cut-off velocity), since J7/3 likely removed most of them. Only 10 asteroids or so seem to be located just behind (on the left) or inside the J7/3, while the total number of bodies between 2.96 and 2.98 AU (on the right side) is 535. At H>14 mag the ratio of populations between 2.94 and 2.96 AU and 2.96 and 2.98 AU would be near unity, if there would be no resonance, asteroids could undisturbly drift by Yarkovsky effect and their distribution inside the "Yarko-envelope" would be uniform. (The border of the envelope is below H = 14 mag.) The actual observed ratio of these populations is 2/125 = approx. 2 %.
Only asteroids with absolute magnitude larger than 13 mag (ie. with radius smaller than 4.5 km) were able to reach this zone by the Yarkovsky drift. (We also do not observe any larger asteroids around 2.96 AU.) Thus there might be some large (R > 4.5 km) resonance crossers in our simulations, because we do not have any observational evidence to prove their (non)existence (at least from the (a, H) distribution of Eos family).

Figure 4 - J7/3 resonance crossing probability (the red line). It is a fraction of test particles (of given H), which crossed the J7/3 resonance on low eccentricity in our numerical simulations (each point is a result of one run eos-j73_*). The blue line is the crossing probability of J9/4 resonance, plotted for a comparsion. [ data | PNG | EPS | PS ]
More than 90 - 95 % of bodies were eliminated by the interaction with J7/3 resonance. Smaller (and thus faster drifting) bodies seem to have slightly larger probabilities to cross J7/3 resonance, but the correlation is not so strong and clear as in the case of J9/4. The uncertainities of probability values are large (for J7/3), because often only one TP (out of 50) crossed the resonance. However, the results of the simulations (eg. approx. 5 % probability to cross the J7/3 resonance for a body with H > 14 mag) are in order-of-magnitude agreenment with the ratio of observed population of Eos family members on the right/left sides of J7/3 resonance (ie. approx. 2 %).