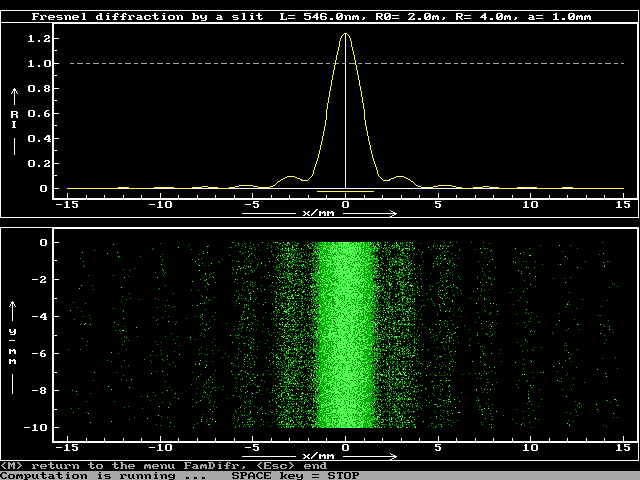
Ukázka z programu difr_b.fm.
Pro MS-DOS je určen soubor famdifr1.zip. Obsahuje DVI soubory, knihovnu fontů, DVI ovladače a dávkové soubory pro prohlížení a tisk publikace Příručka k programovému kompletu FamDifr, anglicke verze Guide Book for the Program Ensemble FamDifr, příručky k programu Difrakční jevy a anglické verze Diffraction phenomena. Rozbalte archiv příkazem unzip famdifr1. Pokud chcete tisknout difraktografické album, musíte nahrát také soubor famalbum.zip rozbalit ho a přesunout do stejného adresáře.

Ukázka z programu difr_b.fm.
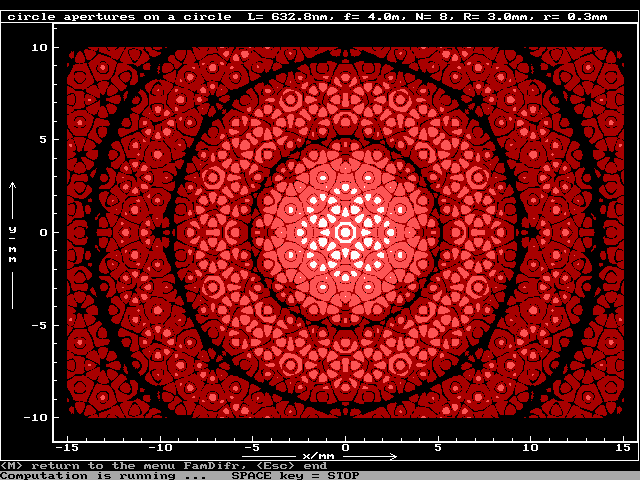
Ukázka z programu difr_m.fm.
Programový komplet FamDifr slouží k modelování výsledků fyzikálních pokusů z vlnové optiky, při kterých demonstrujeme difrakci (ohyb) světla na různých překážkách. Počítačové modely mohou velmi dobře doplnit reálné difrakční pokusy prováděné v hodinách experimentální fyziky a v laboratorních cvičeních. Srovnáním modelů s výsledky pokusů ověříme přesvědčivě platnost fyzikálních zákonů, které difrakční jevy popisují. Komplet FamDifr může být ovšem použit i pro samostatné studium nebo opakování a procvičování učiva a pro přípravu různých studijních materiálů (obrázky jevů, grafy, tabulky).
Modelované situace jsou jednoduché a modelům snadno porozumí i studenti středních škol. Výpočty modelů, které jsou podrobně popsány v třetí kapitole této příručky, však rámec střední školy poněkud překračují a předpokládají některé vysokoškolské znalosti z fyziky a matematiky (teorie elektromagnetického pole, komplexní symbolika pro popis kmitavých dějů, plošný integrál a jeho vyčíslení numerickými metodami). Třetí kapitola je tedy určena především učitelům fyziky a studentům s určitou matematickou průpravou.
Modelované difrakční jevy dělíme na Fresnelovy a Fraunhoferovy. Uživatel si může vybrat z následující nabídky:
| Druh jevu | Překážka |
| Fresnelova difrakce | polorovina |
| (bodový nebo štěrbinový monochromatický zdroj) | štěrbina |
| drát | |
| dvojštěrbina | |
| Fresnelova difrakce | kruhový otvor |
| (bodový monochromatický zdroj) | kruhový terčík |
| Fraunhoferova difrakce | štěrbina |
| (štěrbinový monochromatický zdroj) | řada štěrbin |
| Fraunhoferova difrakce | obdélníkový otvor |
| (bodový monochromatický zdroj) | řada obdélníkových otvorů |
| kruhový otvor | |
| řada kruhových otvorů | |
| kruhové otvory na kružnici | |
| zvolené kruhové otvory | |
| Fraunhoferova difrakce | štěrbina |
| (štěrbinový složený zdroj) | řada štěrbin |
Před každým výpočtem se zadávají rozměry experimentální aparatury v mezích obvyklých při demonstračních pokusech. Vzdálenost stínítka od zdroje světla bývá několik metrů, rozměry difrakční překážky měříme v milimetrech. Zobrazovaná část stínítka je velká 30 krát 20 mm, je tedy o něco menší než políčko kinofilmu. Vlnovou délku světla volíme v intervalu od 200 nm do 1000 nm. Některé jevy se dají modelovat i ve světle složeném ze tří monochromatických světel. Barva modelu na obrazovce počítače přibližně odpovídá barvě světla o zvolené vlnové délce (v případě infračerveného a ultrafialového světla je model černobílý).
Fresnelova difrakce se demonstruje v uspořádání podle obr. 1-1. Mezi bodový zdroj světla a stínítko vložíme pouze difrakční překážku, jejíž šířka je malá v porovnání se vzdálenostmi překážky od zdroje a od stínítka. Pokud je překážkou polorovina, drát, štěrbina nebo několik rovnoběžných štěrbin, můžeme použít i štěrbinový zdroj světla rovnoběžný s překážkou.
Model Fresnelova difrakčního jevu zobrazuje graf relativní intenzity ozáření uprotřed stínítka a vzhled stínítka v oblasti geometrického stínu a jeho blízkého okolí. Hranice geometrického stínu je vyznačena na okraji modelu. Intenzita ozáření I v různých místech modelu je znázorněna tečkováním. Hustota teček závisí na relativní intenzitě ozáření I/I0, kde I0 je intenzita ozáření stínítka před vložením překážky. Nejjasnější místa jsou "přeexponována".
Fraunhoferova difrakce se demonstruje v uspořádání podle obr. 1-2, kde na difrakční překážku dopadají rovinné vlnoplochy, nebo podle obr. 1-3, kde se difrakční překážka umisťuje do sbíhavého světelného svazku.
Pokud je ohnisková dálka f v prvním uspořádání stejná jako vzdálenost difrakční překážky od stínítka d v druhém uspořádání, je výsledný interferenční jev na stínítku v obou případech stejný. V programech kompletu FamDifr předpokládáme uspořádání podle obr. 1-2.
V modelech Fraunhoferovy difrakce je rozložení světelného záření dopadajícího na stínítko znázorněno (podle volby uživatele) tečkováním nebo tónováním. První způsob je vhodný u jednoduchých modelů, druhý použijeme u modelů složitějších s velkým počtem detailů.
Při Fraunhoferově difrakci naměříme největší intenzitu ozáření uprostřed stínítka. Chceme-li v modelu zachytit i mnohem slabší vedlejší maxima interferenčního jevu, musíme relativní intenzitu ozáření I/IM zobrazit až do hodnoty 10-5.
Pokud znázorňujeme relativní intenzitu tečkováním, volíme hustotu teček úměrnou druhé odmocnině z relativní intenzity a celý model poněkud "přeexponujeme". Při tónování se vychází z logaritmické stupnice relativních intenzit ozáření.
Fraunhoferovu difrakci na štěrbině a na řadě rovnoběžných štěrbin můžeme modelovat i ve světle složeném ze tří monochromatických světel o vlnových délkách 430 nm, 540 nm a 650 nm. Relativní intenzita ozáření je u těchto modelů znázorněna pouze tečkováním, přičemž hustota teček je přímo úměrná relativní intenzitě ozáření a celý model je poněkud "přeexponovaný".
Programový komplet FamDifr vznikl přepracováním samostatného programu DIFRAKČNĺ JEVY (autoři Přemysl Šedivý a Vladimír Arnošt, dodává B&BjL Hradec Králové, Markovická 669). Nabídka modelovaných situací je stejná a také vzhled modelů je velmi podobný. Program Difrakční jevy lze použít samostatně a jeho předností je velká rychlost výpočtu ve srovnání s kompletem FamDifr a bohatší barevná paleta. Struktura programu je však pevně dána a použité algoritmy jsou před uživatelem skryty.
Naproti tomu FamDifr je komplet jednoduchých programů, které mohou být samostatně použity v systému Famulus. Jejich struktura je přístupná v editoru a může být uživatelem studována a případně i upravena podle jeho potřeb. Část kompletu je věnována popisu matematických funkcí použitých při výpočtech. FamDifr využívá všech možností, které Famulus poskytuje pro prohlížení modelů a grafů (transfokace, čtení hodnot z grafu pomocí záměrného kříže apod.) a pro jejich reprodukci pomocí tiskárny.
Program DIFRAKČNĺ JEVY a komplet FamDifr se vhodně doplňují.
Instalace programového kompletu je velice jednoduchá. Z distribuční diskety spusťte instalaci příkazem A:\INSTALL nebo B:\INSTALL. V instalačním programu zvolte disk a adresář, kde máte uložen Famulus, kde jsou uloženy knihovny a kam chcete programový komplet instalovat.
Programový komplet FamDifr můžete spustit jedním z následujících způsobů:
Po spuštění programu zadáte vlnovou délku světla, rozměry aparatury a další volby. Nápověda se zobrazuje na spodním řádku.
Graf číslo 1 ukazuje vzhled stínítka. Některé programy zobrazují i graf číslo 2, který znázorňuje rozložení relativní intenzity ozáření v ose $x$. U Fresnelových difrakčních jevů je pod osou $x$ vyznačena žlutou barvou hranice geometrického stínu. Chcete-li zobrazit pouze graf číslo 1 nebo 2, přerušte výpočet stiskem $\langle$Esc$\rangle$ a z hlavního menu Famula zvolte jiné rozložení grafů na obrazovce.
U modelů Fresnelovy difrakce na kruhovém otvoru a terčíku trvá výpočet poměrně dlouho, proto je umožněno výsledky výpočtu pro dané zadání uložit a při dalším spuštění je načíst.
Výpočet můžete kdykoliv přerušit stiskem klávesy Esc, stiskem klávesy E skočit do editoru a podívat se do programu. Ten je psán přehledně a s mnoha komentáři. Stlačené bloky můžete expandovat stiskem Ctrl-E.
Program modelující difrakční jev se skládá z několika částí, které obsahují:
K dispozici je seznam souborů programového kompletu FamDifr seznam souborů programového kompletu FamDifr se stručnou charakteristikou a výčet procedur a funkcí z knihoven.
| DIFR.FML | - | základní knihovna pro komplet FamDifr (výpočet Cornuovy spirály, Besselovy funkce, nastavení barev, grafů) |
| GRAF3D.FML | - | knihovna pro vykreslení dvojrozměrného pole do 3D grafu (škálování, stínování) |
| DIFR_A.FM | - | Fresnelova difrakce na polorovině |
| DIFR_B.FM | - | Fresnelova difrakce na štěrbině |
| DIFR_C.FM | - | Fresnelova difrakce na drátu |
| DIFR_D.FM | - | Fresnelova difrakce na dvojštěrbině |
| DIFR_E.FM | - | Fresnelova difrakce na kruhovém otvoru |
| DIFR_F.FM | - | Fresnelova difrakce na kruhovém terčíku |
| DIFR_G.FM | - | Fraunhoferova difrakce na štěrbině |
| DIFR_H.FM | - | Fraunhoferova difrakce na řadě štěrbin |
| DIFR_I.FM | - | Fraunhoferova difrakce na obdélníkovém otvoru |
| DIFR_J.FM | - | Fraunhoferova difrakce na řadě obdélníkových otvorů |
| DIFR_K.FM | - | Fraunhoferova difrakce na kruhovém otvoru |
| DIFR_L.FM | - | Fraunhoferova difrakce na řadě kruhových otvorů |
| DIFR_M.FM | - | Fraunhoferova difrakce na kruhových otvorech na kružnici |
| DIFR_N.FM | - | Fraunhoferova difrakce na zvolených kruhových otvorech |
| DIFR_O.FM | - | Fraunhoferova difrakce na štěrbině s trojbarevným zdrojem |
| DIFR_P.FM | - | Fraunhoferova difrakce na řadě štěrbin s trojbarevným zdrojem |
| DIFR_3DE.FM | - | Fresnelova difrakce na kruhovém otvoru - 3D graf |
| DIFR_3DF.FM | - | Fresnelova difrakce na kruhovém terčíku - 3D graf |
| DIFR_3DK.FM | - | Fraunhoferova difrakce na kruhovém otvoru - 3D graf |
| DIFR_3DL.FM | - | Fraunhoferova difrakce na řadě kruhových otvorů - 3D graf |
| DIFR_VBC.FM | - | Fresnelova difrakce na štěrbinách a drátech různé velikosti |
| CORN.FM | - | vykreslení Cornuovy spirály - klotoidy |
| BESSEL.FM | - | výpočet Besselovy funkce |
| FUNKCE_S.FM | - | zobrazení štěrbinové funkce |
| FUNKCE_M.FM | - | zobrazení mřížkové funkce |
| INFO.FM | - | informace o difrakčních jevech (odpovídá 1. kapitole příručky) |
| MENU.FM | - | volání ostatních programů z přehledných nabídek |
| DIFR_E1.DAT | - | Fresnelova difrakce na kruhovém otvoru - vypočtené relativní intenzity |
| DIFR_E2.DAT | - | Fresnelova difrakce na kruhovém otvoru - vypočtené relativní intenzity |
| DIFR_F1.DAT | - | Fresnelova difrakce na kruhovém terčíku - vypočtené relativní intenzity |
| CTI.MNE | - | poznámky ke spouštění |
| SOUBORY.FMN | - | seznam souborů programového kompletu FamDifr |
PROCEDURE Corn(REAL L,R0,R); REAL FUNCTION CornX(INT n); REAL FUNCTION CornY(INT n); PROCEDURE Bessel(REAL L,f,a); PROCEDURE NastavBarvy(REAL L,VAR INT Barva1,Barva2);Knihovna GRAF3D obsahuje procedury pro zobrazení dvojrozměrného pole do třírozměrného grafu. Pro popis grafu a škálování os je využita knihovna SCALEAX, která je standartně dodávána s Famulem. Bližší popis procedur je k dispozici v samotné knihovně.
PROCEDURE SetGraph3D( INT GrNo ); PROCEDURE SetColor3D( INT Color1,Color2 ); PROCEDURE SetBox3D( x,y,z ); PROCEDURE SetView3D( azimut,vyska ); PROCEDURE SetLight3D( azimut_svetla,vyska_svetla ); PROCEDURE SetShadow3D( INT MinRastr,MaxRastr ); PROCEDURE SetScale3D( BOOLEAN skalovat ); PROCEDURE SetAxis3D( INT Color,Font, CHAR nadpisx[],nadpisy[],nadpisz[] ); PROCEDURE Array3D( z[i=mini TO maxi,j=minj TO maxj],minx,maxx,miny,maxy );