First we started numerical integration of motion, we have to choose appropriate numerical method. We expect changes of major semiaxis in order of 0.001 AU/Myr due to Yarkovsky diurnal effect. Numerical errors should be sufficiently smaller. I developed program mptest.f which tests several methods by integrating a two body problem, The changes of elements of orbit are produced only by cumulation of local numerical errors.
We excluded simple methods without time step (local relative error) control (Runge - Kutta 4th order, Hamming predictor - corrector method, Adams - Moulton method). The reason is substancial dependence of local relative error on eccentricity of orbit, this element would change rapidly due to gravitational resonances.
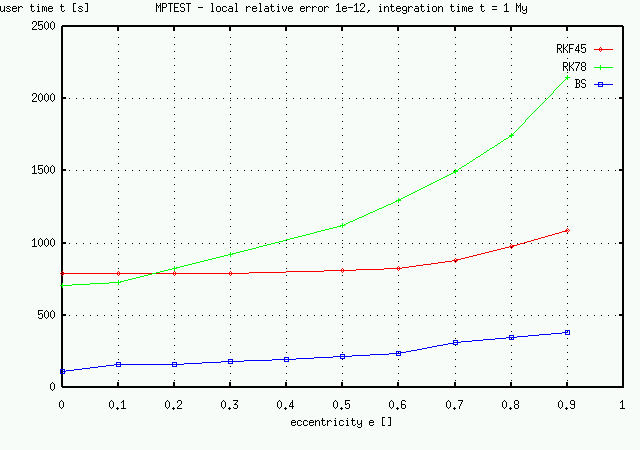
A comparsion of three methods is presented in following graphs:
As a result of this testing I found BS method with local relative error 10-14 to be optimal for our calculations.

| Notice a strong dependence of calculation time on eccentricity for method RK78. BS method is several times faster, but its accumulated global error is greater. The solution would be to decrease local relative error downto 10-14, as you can see below. |
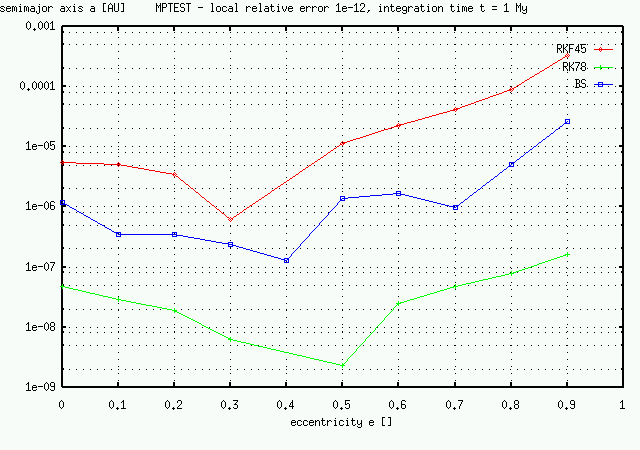
| A strange dependence of global error represented by change of semimajor axis on eccentricity. All three methods are equivalent, but they have a different order and this fact leads to differences in global errors. |
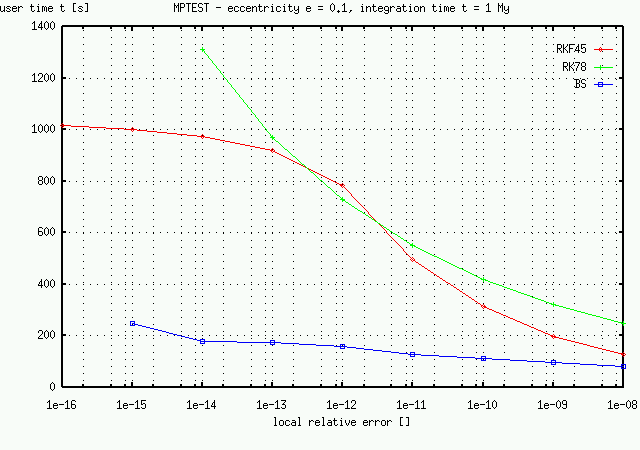
| Here you can see the most important advantage of BS method - decrease a local relative error with only a slight increase of calculation time. This is not true for RKF45 method due to saturation of global error (see below). |
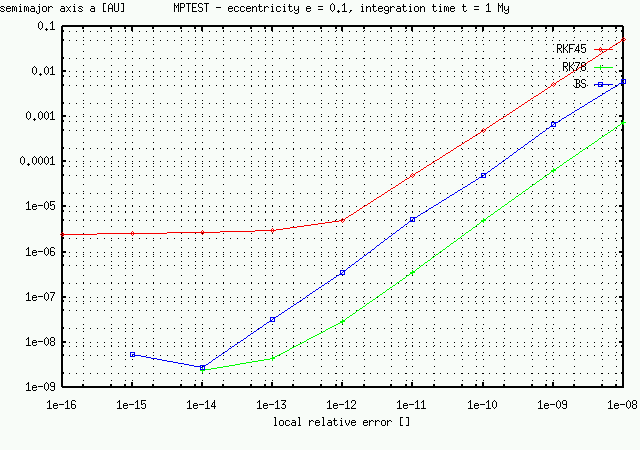
| Clearly visible saturation of RKF45 method - you cannot decrease global error, because this method has too low order. On the other hand BS method will be equivalent to RK78 for local relative error 10-14. |