


(e, sin I)

If you do not agree with any of these numbers, please let me know! :)
See also notes on individual families. You can download datafiles for old/big or new families here.
 |
 |
 (e, sin I) |
There are however several potential problems:
This very choice may however affect results substantially! A profound example is the Teutonia family which contains also BIG asteroid (5) Astraea in the synthetic catalogue but it does NOT in case of the semi-analytic catalogue (because the eccentricity of Astraea is different: e = 0.2279 vs 0.1980486). Physical properties of the family then differ vastly, of course!
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Sizes of symbol correspond to the sizes of asteroids, black symbols emphasize large bodies and red circles are positions of the largest bodies of known families. In the second row, we see a colour-coded Sloan colours instead.
Do you think that it is worth to identify all of them? Well, most of them consists of small bodies and they are likely young...
Possibly, only the following 16:
# dsg name v_cutoff N_members p_V tax. D_PB D_PB (SPH) LF/PB v_esc slope_1 slope_2 age refs
(I am running some simulations to get additional age estimates. A preliminary information is given by the C-parameter inferred from the (a,H) plot.)
It is really suspicious that most "possibly-LHB" families are larger than D_PB =~ 200 km. We then have to ask ourselves: Where are the families with D_PB =~ 100 km?!
| excluding cratering | |
 |
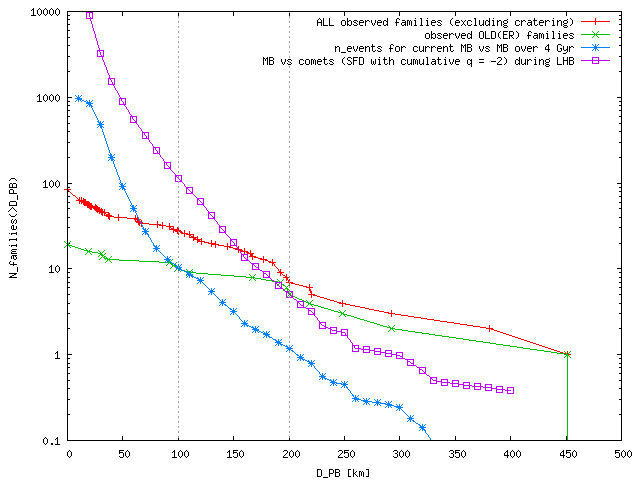 |
The cumulative number of families with D_PB > D and expected number of events for MB vs MB collisions and MB vs comets (with cumulative q_2 = -2). Note the slopes of these dependences are very different, especially in between D = 100 and 200 km! (Small families do not matter, since they likely disperse quickly, so we can see only recent ones.)
The list of old families excluding cratering events is attached here:
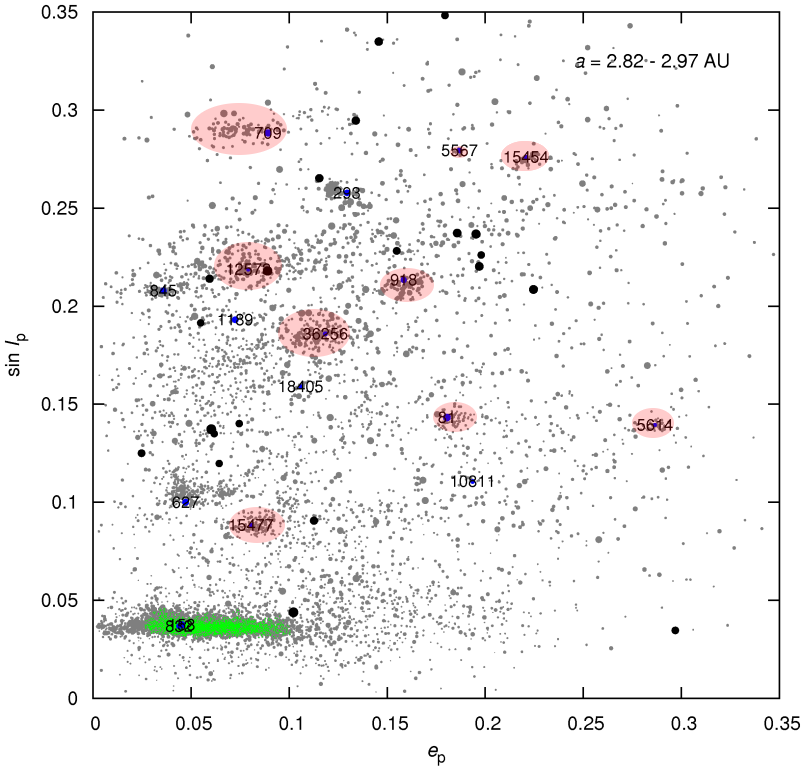
Let's now focus on the zone a = 2.825 - 2.955 AU, i.e. the so called "pristine Main Belt" as it probably looked in the past.
About 9 new small families are visible on the (e, sin I) plot and they are confirmed by SLOAN colours too! Nevertheless, there is only one big family in this zone, i.e. the Koronis. See the discussion of this intriguing fact below...
 |
 |
 colour code |
How many families would be created in the Main Belt if we use a "classical" SFD for comets (Vokrouhlicky, Nesvorny & Levison 2008)? Typically, the intrinsic collisional probability and the collisional velocity evolve like this:

Since the average impact velocity is V_imp =~ 10 km/s, we need the following projectile sizes:
| D_target [km] | N_targets in the MB | Q^star_D [J/kg] | d_disrupt [km] | for rho_target/rho_project = 3.0/0.5 |
| 100 | ~192 | 1e5 | 12.6 | 23 |
| 200 | ~23 | 4e5 | 40.0 | 73 |
If we try to use the following SFDs (with various q_1, q_2, D_0):

we end-up with the following number of disruption events in the Main Belt:
| differential | ||||||
| q_1 | q_2 | D_0 [km] | M_disk [M_E] | n_events for D_PB >= 100 km | n_events for D_PB >= 200 km | notes |
| 5.0 | 3.5 | 50 | 35 | 189 | 3.9 | steep SFD |
| 5.0 | 2.5 | 50 | 35 | 134 | 6.5 | nominal case |
| 5.0 | 2.0 | 50 | 35 | 99 | 7.0 | |
| 5.0 | 1.5 | 50 | 35 | 73 | 7.3 | |
| 5.0 | 1.1 | 50 | 35 | 59 | 7.5 | extremely shallow SFD |
| 4.0 | 2.5 | 50 | 35 | 84 | 4.4 | different q_1 |
| 5.0 | 2.5 | 70 | 35 | 84 | 5.2 | larger turn-off |
| 5.0 | 2.5 | 50 | 10 | 38 | 1.9 | lower M_disk |
| 5.0 | 2.5 | 50 | 35 | 104 | 4.2 | V_imp = 8 km/s |
| 5.0 | 2.5 | 50 | 35 | 163 | 8.9 | V_imp = 12 km/s |
| 5.0 | 3.0 | 100 | ~45 to 17 | 115 to 34 for rho_t/rho_p = 3.0/0.5 | 4.9 to 1.2 | Morby's case (10^8 bodies with D = 100 km, cumul. slope -2) |
| 5.0 | 2.5 | 150 | 35 | 28 to 11 | 2.1 to 0.7 | even larger turn-off |
| extreme cases | ||||||
| 5.0 | 2.5 | 50 | 35 | 448 | 32 | Q^star_D = 10^4 J/kg |
| 5.0 | 0.0 | 70 | 10 | 4.1 | 1.2 | "worst case" with zero q_2 |
It is clearly contradicting the observations, since we observe almost no LHB families with D_PB =~ 100 km! Moreover, this result is robust with respect to the slope q_2, even very shallow distributions produce a lot of families. (The "worst case" with q_2 = 0.0 is not likely at all, e.g. because of continuous SFD of basins on Iapetus and Rhea, which exhibits only a mild depletion of ~100-km size craters; see Kirchoff & Schenk (2010). On the other hand, Sheppard & Trujillo (2010) report an extremely shallow cumulative SFD of Neptune Trojans which is akin to low q_2.)
Nevertheless, it may be possible that approx. 5 LARGE families with D_PB =~ 200 km (which are indeed observed) are of LHB origin? BUT it would be very strange that several D_PB =~ 200 km families exist and D =~ 100 km families do NOT exist at all at the same time, because the projectiles capable to disrupt a LARGE parent body is of course capable to disrupt a small one too.
BTW, is it theoretically possible that the TARGET (main-belt) population had a peculiar SFD with essentially NO D =~ 100 km bodies and ONLY D =~ 200 km bodies were present?! This might solve the problem with no 100 km-size AND several 200 km-size families...

As you can see, there is almost zero (<0.001) probability that the number of families in the "pristine MB" is zero or one. Mostly, we get 8 families there. We may also ask the other way: what is the maximum number of LHB disruptions which would allow zero or one family in the "pristine MB"? That is shown in the following figure:
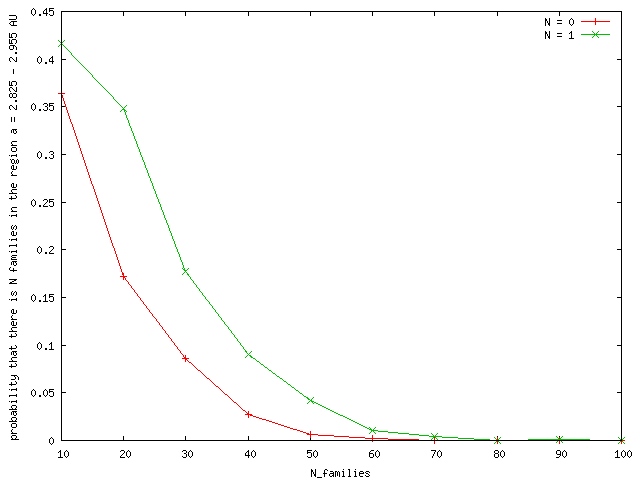
The result is that the maximum number of disruptions is about 60 to get zero or one family in the "pristine MB" with a >0.01 probability.
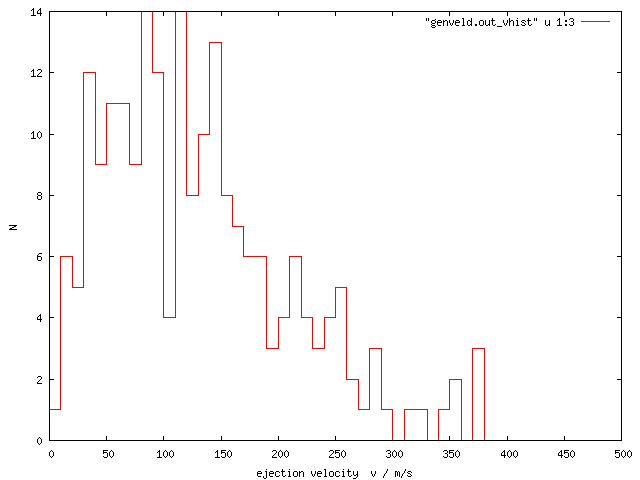
Let's take D = 100 km parent bodies, and assume a size-dependent ejection velocity V ~ 1/D (V = 50 m/s for D = 5 km) with the size distribution that of the Koronis family.
See the following figures. The answer to the question is then simple: the families do not overlap too much and they cannot be hidden that way!
| large asteroids only (D > 10 km) | Koronis-like SFD downto D =~ 2 km | |
| v_eject |  |
 |
| (a, e) | 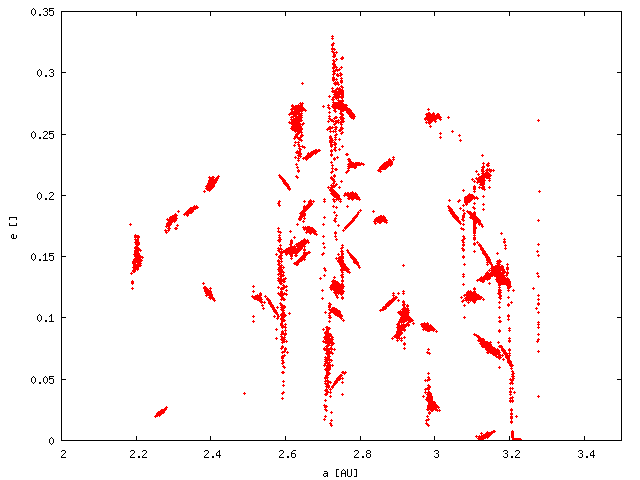 |
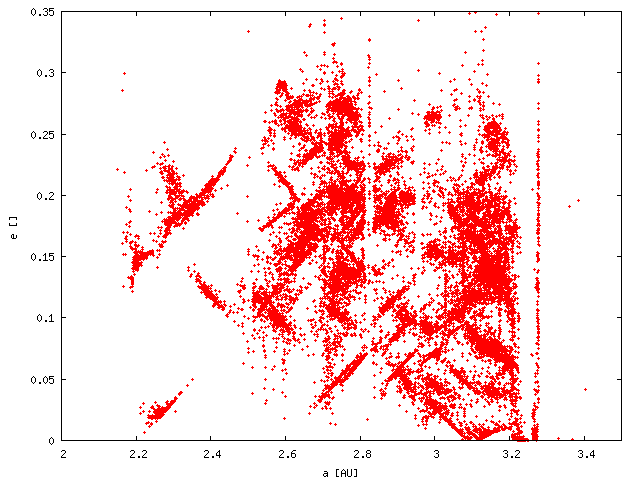 |
| (a, sin I) | 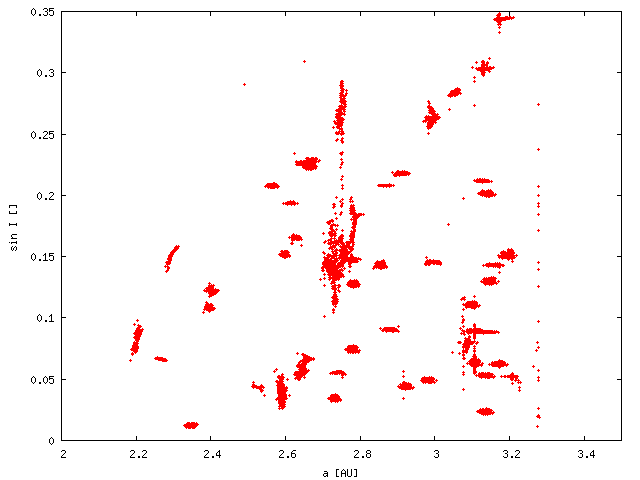 |
 |
This is a simplest Monte-Carlo approach, i.e. there is the Yarkovsky drift in semimajor axis da/dt multiplied by 4 Gy and also evolution of eccentricities and inclinations due to interactions with mean-motion and secular resonances. To account for this we integrated one family in the outer belt upto 4 Gyr and estimated the drifts in all elements a, e, sin I. Well, we actually speeded-up the integration by dividing diameters by 10 and integrating upto 0.4 Gyr only:
 |
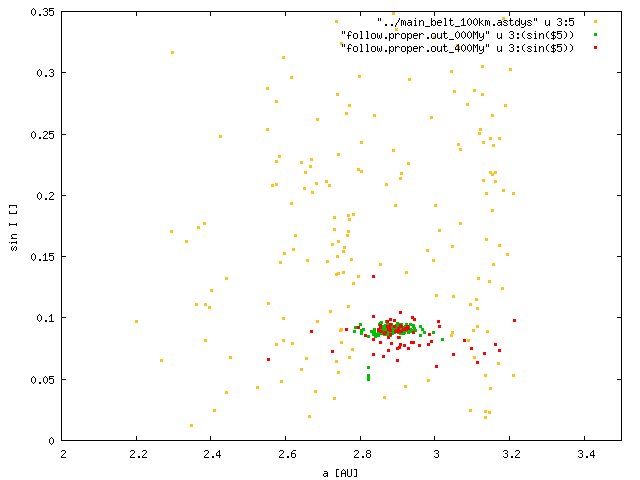 |
Then, we assigned drifts randomly to each member of 100 families, respecting asteroid sizes of course. Because this Monte-Carlo approach tends to smear all structures, we regard the following plots as the "upper limits" for dispersion.
Results: Eccentricities of small asteroids seem to be dispersed enough to hide any families, but there are still some persistent structures in inclinations, which are not observed. Moreover, large asteroids seem to be clustered even after 4 Gyr. We thus can conclude that it is not possible to disperse the families by the Yarkovsky effect alone!
| large asteroids only D > 10 km | Koronis-like SFD downto D =~ 2 km | |
| (a, e) | 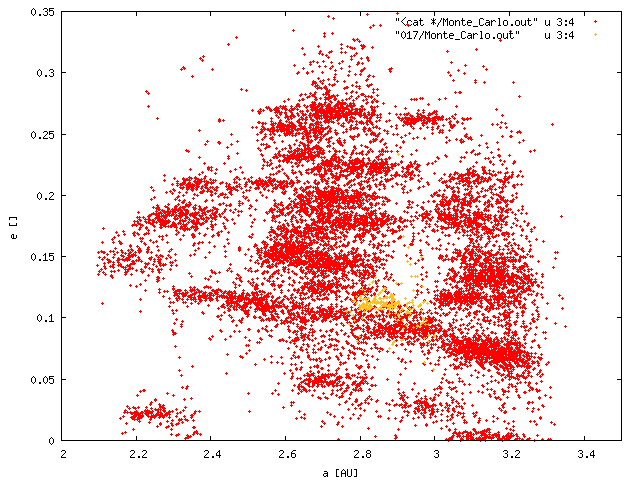 |
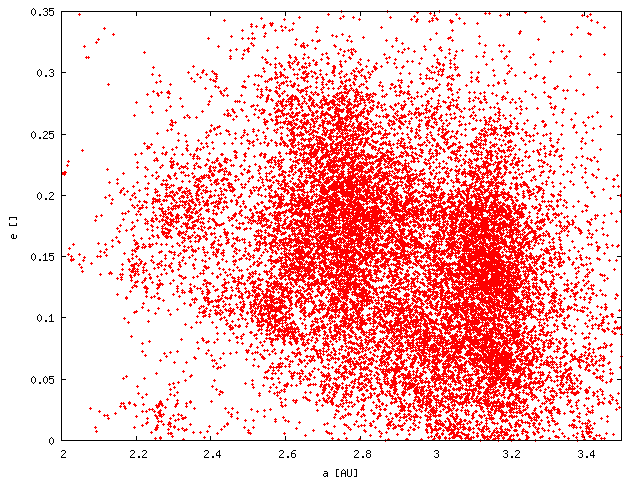 |
| (a, sin I) | 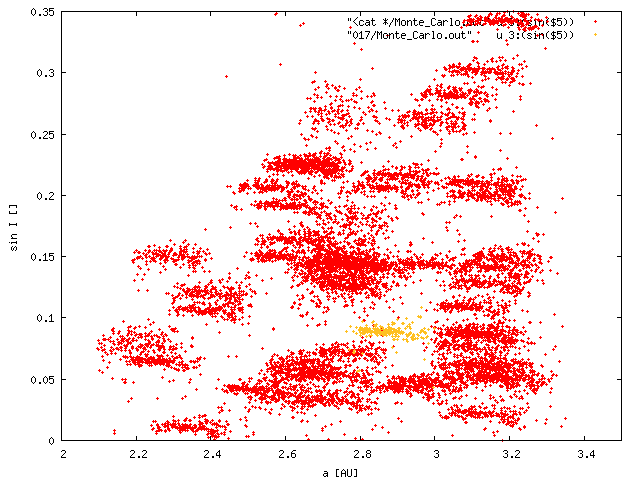 |
 |
We restarted one of the cometary-disk integrations with a fine sampling of the output (dt_out = 500 yr). Then we processed the output and calculated the intrinsic impact probabilities P_i including a simple comet-disruption criterion: q < q_crit = 1.5 AU. This is likely an upper limit for disruptions, since the probability of disruption is p_crit = 1 in this particular case, but it may be lower (and q-dependent) in reality.
As we can see in the following figures, the P_i's are then decreased ONLY by a factor ~3. Another factor is ~1.5 due to systematically lower mean impact velocities V_imp which decrease from 12 km/s to 8 km/s, but this is again not substantial in terms of the resulting number of events (i.e. ~4.5 times lower). Conclusion: disruptions of comets cannot decrease the number of projectiles sufficiently!
| P_i | 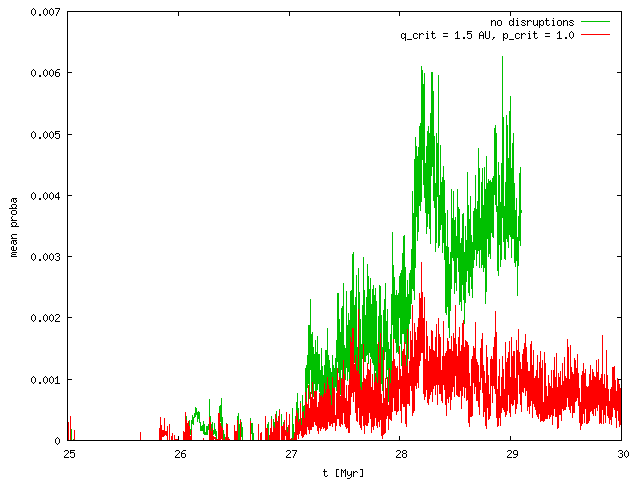 |
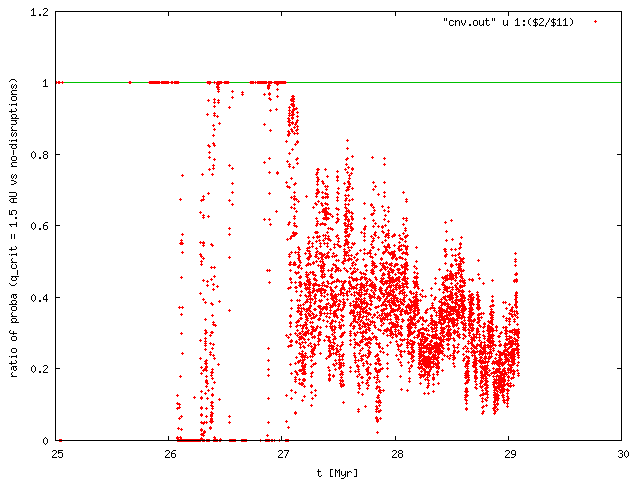 |
| V_imp | 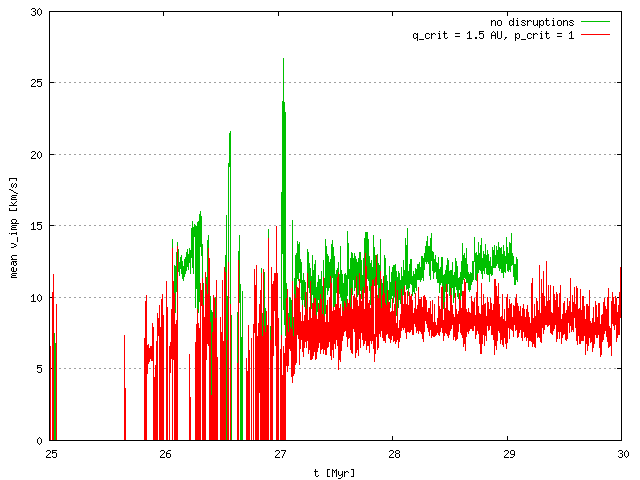 |
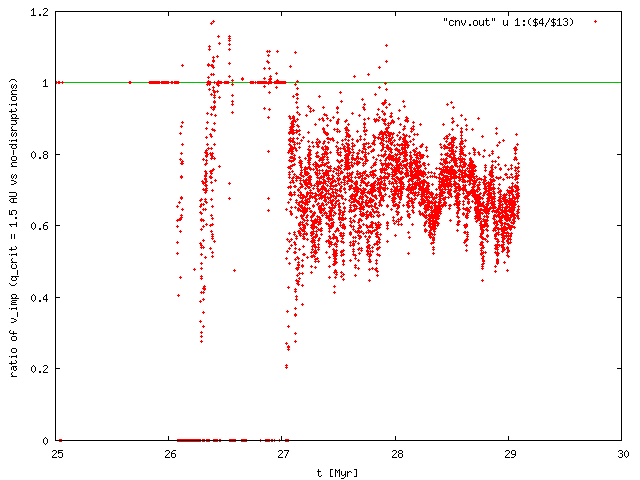 |

A histogram of the total dynamical lifetimes of comets in our simulation (red line) compared to the "physical" lifetimes which include the q < q_crit = 1.5 AU criterion (green line). They do not differ very much, but some of the long-lived orbits change to short-lived due to the criterion, so the effect on P_i probabilities is more substantial. Only orbits colliding with the Main Belt are considered.
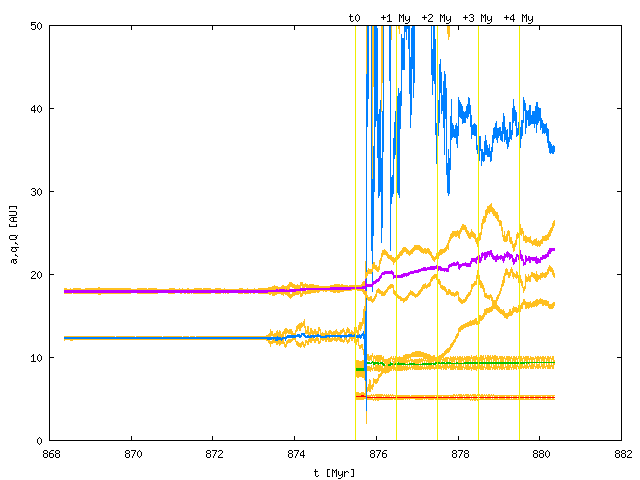
We obtained the following orbital evolution of planets from Morby:
| Jupiter | Saturn | |
 |
 |
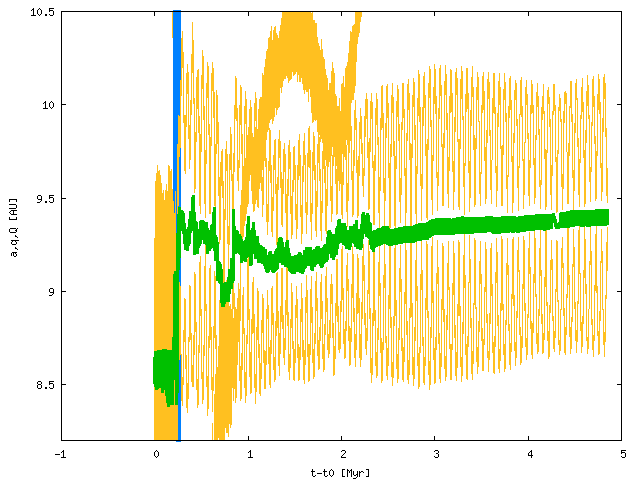 |
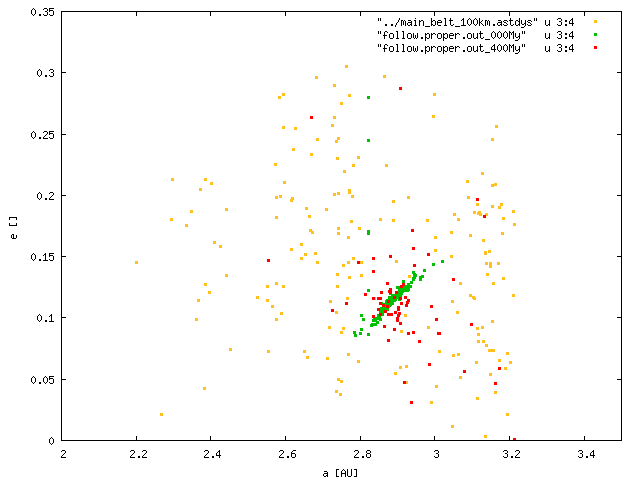
We then used a modified SWIFT integrator, which reads orbital elements for planets from an input file and calculates only the evolution of test particles. We decided to study one of the synthetic families with low e and I. (We are going to run a few more simulations in the inner/middle/outer belt.)
We start the evolution of planets at various times, ranging from t_0 = 878.5 My to (t_0 + 4 My) and we stop the integration at (t_0 + 4 My). Finally, we calculate proper elements when the planets do not migrate anymore. The results are shown below:
One has to be aware during the follow-up calculation of proper elements, because planets may still become unstable! We should move planets smoothly to their exact current orbital positions (using the same code as before). Note that high-inclination families would be dispersed by the Kozai mechanism (eccentricities are perturbed by slightly migrating or overlapping mean-motion resonances and this is translated to I's).
The families at low e and I do not seem to be dispersed enough during later stages of the giant-planet migration. Even though we do not have a precise timing of the impactor flux yet (Rodney Gomes?), we can expect most comets arrive between t_0 and (t_0 + 2 My), because Neptune migrates only relatively slowly later on. So most families created early on would NOT be perturbed enough to disappear.
Conclusion: It is NOT possible to destroy low-e and -I families by planetary migration!
Note that the today-non-existent families around (107) Camilla and (121) Hermione - inferred from the existence of their satellites - cannot be destroyed in the jumping-Jupiter scenario, unless the families were actually pre-LHB and experienced the jump!
Collisions between hard targets (rocky asteroids) and extremely weak projectiles (active icy comets) at high impact velocities V_imp =~ 12 km/s may have a very different physics (Patrick Michel?). Note that comets sometimes disintegrate from internal/outgassing reasons (i.e. WITHOUT any collision). The energy consumed by phase transitions may play an important role too?
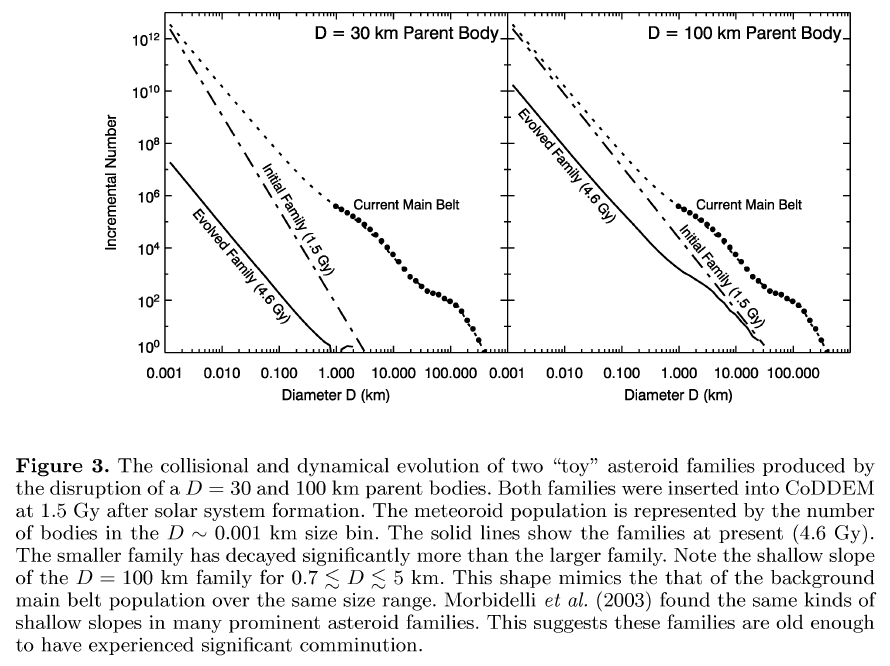
According to Bottke etal (2005) - see Figure - the comminution is NOT sufficient to destroy a D_PB = 100 km family in the current main belt. Most of D > 10 km fragments survive intact. Note that if we decrease Q_D^* the family is more susceptible to comminution BUT we get a lot more families from our model presented in Section 4!
We ran several simulations with the Boulder code. (Beware, these are first trials, so "everything can be wrong"!) We used the following phys_par.dat:
/* /* Q*_D PARAMETERS /* /* bulk rho Q0 a B b rho_Q*, dividing factor /* 3.0d0 7.0d7 -0.45d0 2.1d0 1.19d0 3.0d0 1.0 3.0d0 7.0d7 -0.45d0 2.1d0 1.19d0 3.0d0 1.0and collprob.dat:
/*
/* P_i and Impact Velocity of Projectile (i) on Target (j)
/*
3.10e-18 5.28 annulus 1 vs 1
3.10e-18 5.28 annulus 1 vs 2
3.10e-18 5.28 annulus 2 vs 1
3.10e-18 5.28 annulus 2 vs 2
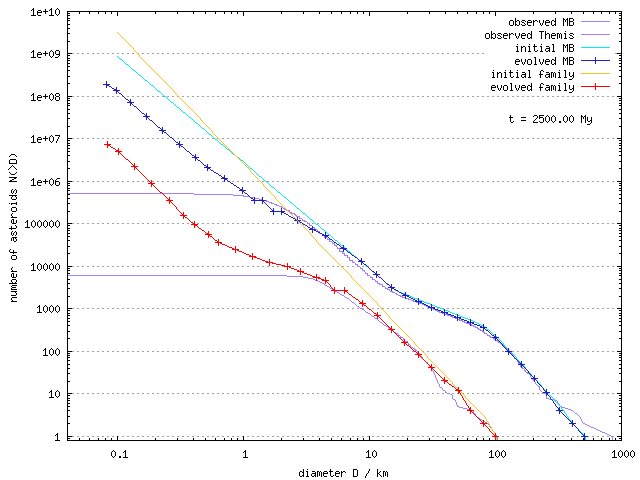
First, we tested the boulder code on the Koronis and the Themis families which are likely 2.5 +- 1.0 Gyr old:
| MB vs Koronis (D_PB = 100 km) | MB vs Themis (D_PB = 200 km) | number of families in the MB |
 |
 |
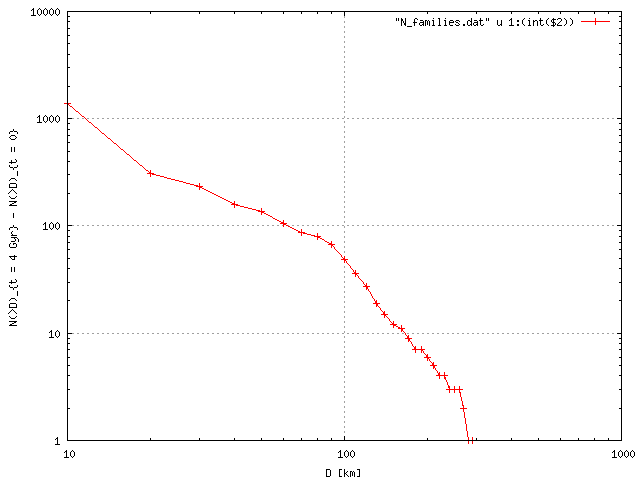 |
Results:
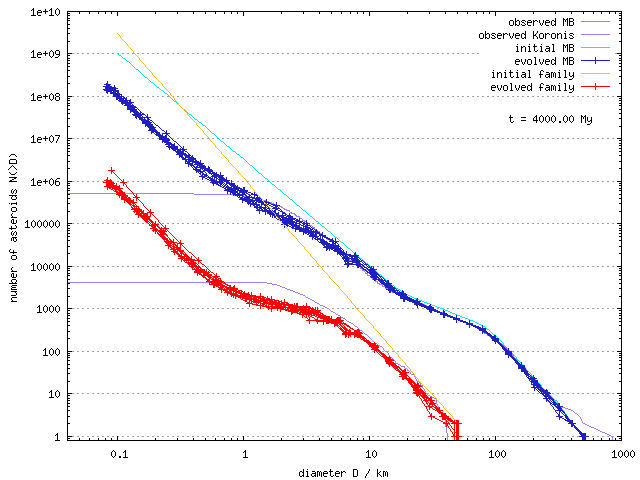
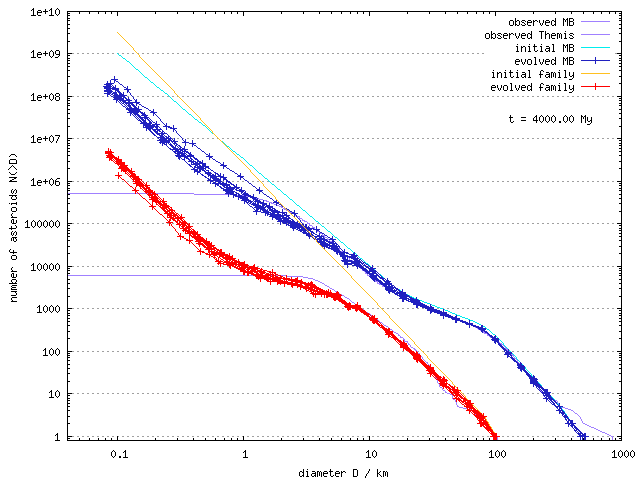
Then, we prepared the following three model situations:
The initial and final SFD's after 4 Gyr of collisional evolution are shown below:
| MB vs 1 family D_PB = 100 km | MB vs 1 family D_PB = 200 km | 2× MB vs 100 families |
 |
 |
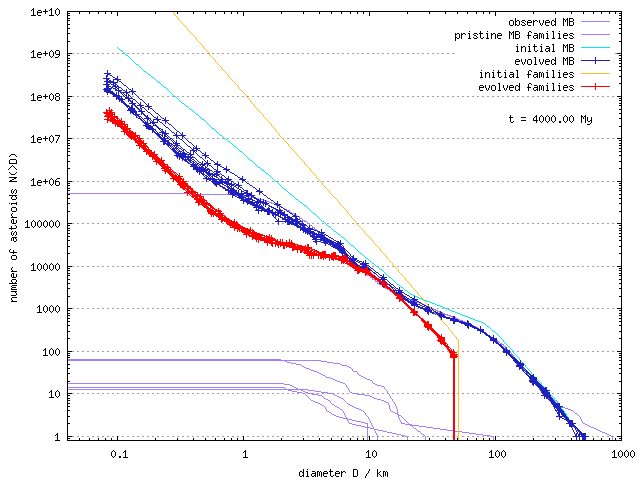 |
The simulations were started multiple times with different random seeds. We started with family SFD's which are steeper than currently observed.
Results:
It is also interesting to note that the resulting family population has a VERY FLAT SFD in the range D = 1 to 10 km - similarly as some of the "less-certain" observed families! May be, the families like (709) Fringilla, (918) Itha, (5567) Durisen, (12573) or (15454) (all from the "pristine MB" zone, ) are actually remnants of LARGER AND OLDER families, even though they are denoted as "younger"?! The (a,H) estimate can be totally wrong since small bodies were destroyed by comminution and spread by the YE far away from the family.
Now we have to ask an important question: How an old/comminutioned family can look like in the proper-element space? To this aim, we created a synthetic family in the "pristine MB", propagated the large asteroids (D > 10 km) up to 4 Gyr due to the YE and then we selected randomly only ONE TENTH of asteroids to simulate strong comminution. Finally, we placed the resulting single family into the "pristine MB" (among other observed families) to get a feeling if it is easily observable:
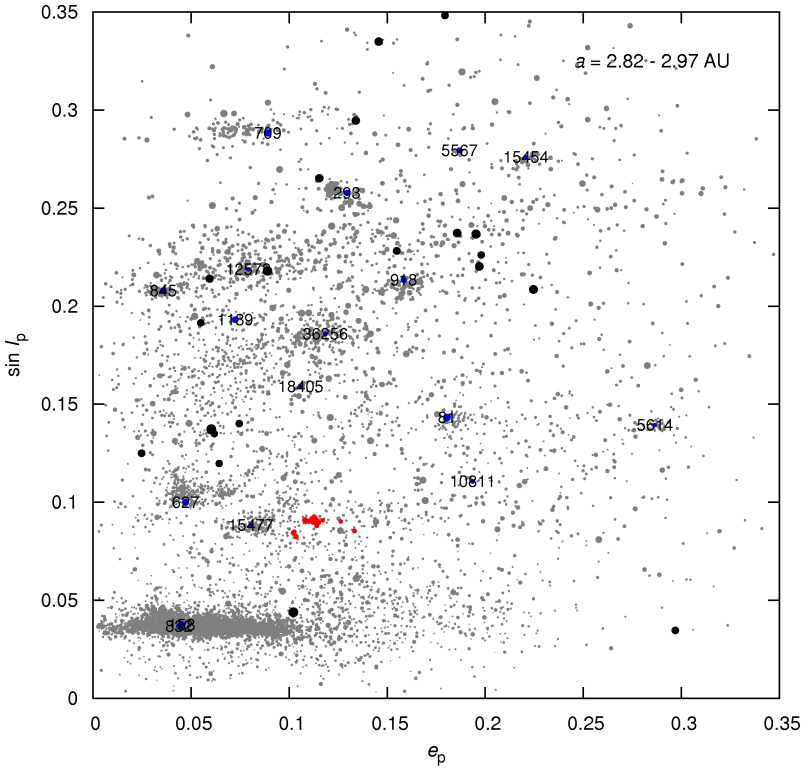 |
The families which are already identified in the proper-element space are denoted by a designation of the parent body. The synthetic old/comminutioned family is denoted by red colour.
See also the family prior comminution or typical dispersion of small bodies.
 |
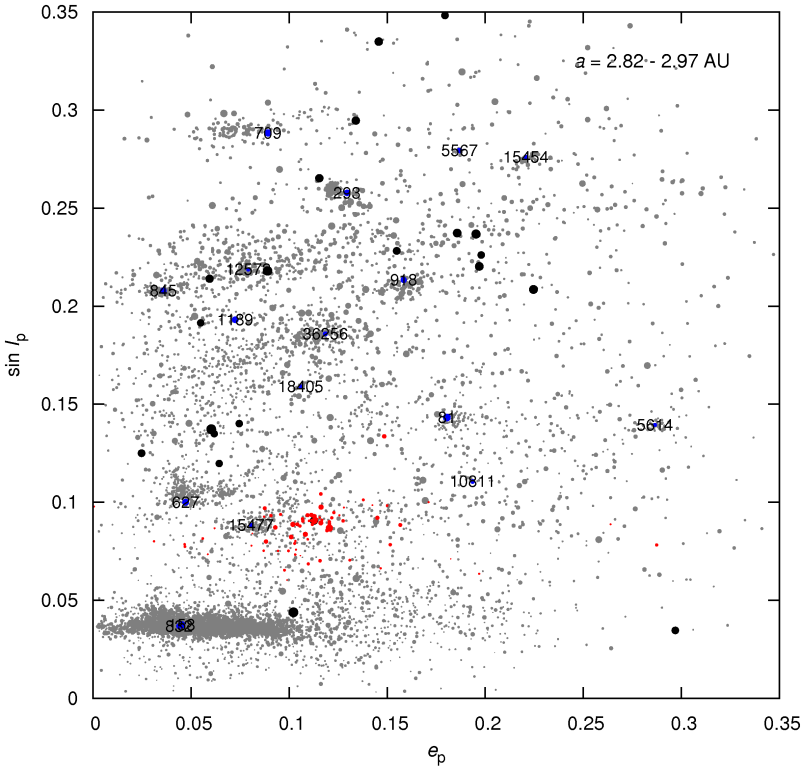 |
It is clear that such family is HARDLY OBSERVABLE even in the almost-empty zone of the MB! Conclusion: the comminution (as given by the Boulder code) CAN EXPLAIN the paucity of D_PB = 100 km LHB families!
Finally, how 100 old/comminutioned families look like compared to the whole main belt? Let's compare D > 10 km bodies only:
| 100 families | including MB | comminution only by factor 3 |
 |
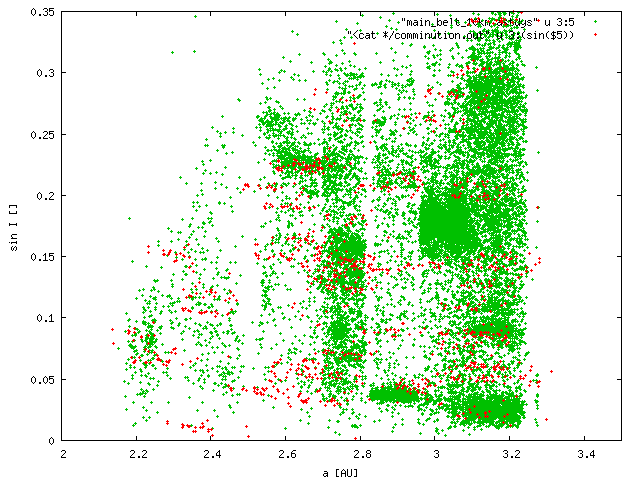 |
 |
Conclusion: If the comminution indeed decreases the number of family members by a factor of 10, we can hardly distinguish old families from background!
The main conclusions are the following: according to a standard model approx ~100 families with D_PB >=~ 100 km should be created in the main asteroid belt during the LHB. Moreover, we expect many more D_PB >= 100 km families than D_PB >= 200 km. Both facts are in a clear contradiction with observations.
The following possibilities seem to be ruled-out:
We are thus left with five explanations (all of them may actually contribute):